A Wavelet Tour of Signal Processing : The Sparse Way
This should be the bible to understand the Wavelet.
Complete theory in match is provided.
A Wavelet Tour of Signal Processing
The Sparse WaySte ́phane Mallat
with contributions from Gabriel Peyré
Preface to the Sparse Edition
Wavelets are no longer the central topic, sparse representation and processing are now at the core.
This book is intended as a graduate-level textbook. Its evolution is also the result of teaching courses in electrical engineering and applied mathematics.
1 Sparse Representations
Processing is faster and simpler in a sparse representation where few coefficients reveal the information we are looking for.
1.1 COMPUTATIONAL HARMONIC ANALYSIS
1.1.1 The Fourier Kingdom
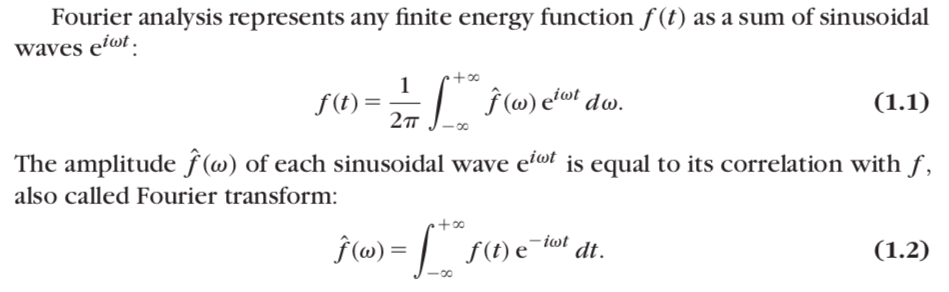
1.1.2 Wavelet Bases
The story began in 1910, when Haar constructed a piecewise constant function

the dilations and translations of which generate an orthonormal basis

Any finite energy signal f can be decomposed by this wavelet orthonormal basis:

The coefficients of the wavelet basis can be obtained by

Each Haar wavelet has a zero average over its support interval. If f(t) is locally regular and the interval is small, then it is nearly constant over this interval and the wavelet coefficient is nearly zero. This means that many wavelet coefficients are located at sharp signal transitions only.
1.2.1 Sampling with Linear Approximations
1.3 TIME-FREQUENCY DICTIONARIES
In signal processing, time–frequency analysis comprises those techniques that study a signal in both the time and frequency domains simultaneously, using various time–frequency representations, time–frequency analysis studies a two-dimensional signal – a function whose domain is the two-dimensional real plane, obtained from the signal via a time–frequency transform.
Motivated by quantum mechanics, in 1946 the physicist Gabor proposed decomposing signals over dictionaries of elementary waveforms which he called time-frequency atoms that have a minimal spread in a time-frequency plane.
The key issue is to understand how to construct dictionaries with time-frequency atoms adapted to signal properties.

留言