Cryptography
Cryptography
just for beginners
tutorialspoint
simplyeasylearning
1. CRYPTOGRAPHY – ORIGIN
History of Cryptography
Caesar Shift Cipher
Evolution of Cryptography
2. MODERN CRYPTOGRAPHY
Characteristics of Modern Cryptography
Context of Cryptography
Cryptography is the art and science of making a cryptosystem that is capable of providing information security.The art and science of breaking the cipher text is known as cryptanalysis.
Security Services of Cryptography
- Confidentiality keeps the information from an unauthorized person.
- Data Integrity deals with identifying any alteration to the data.
- Authentication Message authentication and Entity authentication
- Non-repudiation the original creator of the data cannot deny the creation or transmission of the said data to a recipient or third party.
Cryptography Primitives
Cryptography primitives are nothing but the tools and techniques in Cryptography that can be selectively used to provide a set of desired security services:
3. CRYPTOSYSTEMS
Components of a Cryptosystem
Types of Cryptosystems
- Symmetric Key Encryption The encryption process where same keys are used for encrypting and decrypting the information is known as Symmetric Key Encryption.
- Digital Encryption Standard (DES)
- Triple-DES (3DES)
- IDEA
- BLOWFISH
- Key establishment
- Trust Issue
- Asymmetric Key Encryption The encryption process where different keys are used for encrypting and decrypting the information is known as Asymmetric Key Encryption.
- When Host1 needs to send data to Host2, he obtains the public key of Host2 from repository, encrypts the data, and transmits.
- Host2 uses his private key to extract the plaintext.
A robust mechanism needs to exist to exchange the key between the communicating parties.
Length of Key (number of bits) in this encryption is smaller and hence, process of encryption-decryption is faster than asymmetric key encryption.
Challenge of Symmetric Key Cryptosystem:
It requires to put the public key in public repository and the private key as a well-guarded secret.
Relation between Encryption Schemes
Kerckhoff’s Pri ciple for Cryptosyste
4. ATTACKS ON CRYPTOSYSTEMS
Passive Attacks
The main goal of a passive attack is to obtain unauthorized access to the information.Active Attacks
An active attack involves changing the information in some way by conducting some process on the information.Assumptions of Attacker
Cryptographic Attacks
Practicality of Attacks
5. CRYPTOGRAPHY – TRADITIONAL CIPHERS
Earlier Cryptographic Systems
- All of these systems are based on symmetric key encryption scheme.
- The only security service these systems provide is confidentiality of information.
- Unlike modern systems which are digital and treat data as binary numbers, the earlier systems worked on alphabets as basic element.
Caesar Cipher
Simple Substitution Cipher
Monoalphabetic and Polyalphabetic Cipher
Playfair Cipher
Vigenere Cipher
One-Time Pad
Transposition Cipher
6. MODERN SYMMETRIC KEY ENCRYPTION
A symmetric encryption schemes can be classified in to- Block Ciphers The plain binary text is processed in blocks (groups) of bits at a time; i.e. a block of plaintext bits is selected, a series of operations is performed on this block to generate a block of ciphertext bits.
- Stream Ciphers The plaintext is processed one bit at a time i.e. one bit of plaintext is taken, and a series of operations is performed on it to generate one bit of ciphertext.
The number of bits in a block is fixed.
For example, the schemes DES and AES have block sizes of 64 and 128, respectively.
7. BLOCK CIPHER
- A block cipher takes a block of plaintext bits and generates a block of ciphertext bits, generally of same size.
- The size of block is fixed in the given scheme.
- The choice of block size does not directly affect to the strength of encryption scheme. The strength of cipher depends up on the key length.
Block Size
The selection of a size of a block:- Avoid very small block size
- Do not have very large block size
- Multiples of 8 bit
Padding in Block Cipher
The length of plaintexts is mostly not a multiple of the block size.The last block of bits needs to be padded up with redundant information so that the length of the final block equal to block size of the scheme.
The process of adding bits to the last block is referred to as padding.
Block Cipher Schemes
- Digital Encryption Standard (DES) It is now considered as a ‘broken’ block cipher, due primarily to its small key size.
- Triple DES It is a variant scheme based on repeated DES applications but inefficient compared to the new faster block ciphers available.
- Advanced Encryption Standard (AES)
- IDEA The use of IDEA scheme has a restricted adoption due to patent issues.
- Twofish
- Serpent
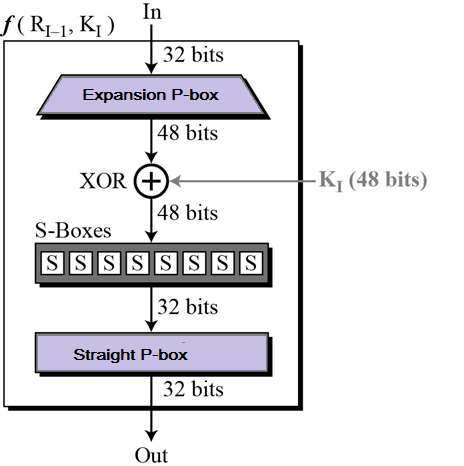
8. FEISTEL BLOCK CIPHER
Feistel Cipher is a design model from which many different block ciphers are derived.The cryptographic system based on Feistel cipher structure uses the same algorithm for both encryption and decryption.
Encryption Process
- The input block to each round is divided into two halves that can be denoted as L and R for the left half and the right half.
- In each round, the right half of the block, R, goes through unchanged. But the left half, L, goes through an operation that depends on R and the encryption key. First, we apply an encrypting function ‘f’ that takes two input - the key K and R.
- In real implementation of the Feistel Cipher, a round-dependent key (a subkey) is derived from the encryption key.
- The number of rounds are specified by the algorithm design.
- Once the last round is completed then the two sub blocks, ‘R’ and ‘L’ are concatenated in this order to form the ciphertext block.
The function produces the output f(R,K).
Then, we XOR the output of the mathematical function with L.
If these are not swapped then the resulting ciphertext could not be decrypted using the same algorithm.
Decryption Process
The ciphertext block is fed in to the start of the Feistel structure and then the process thereafter is exactly the same as the encryption process.The only difference is that the subkeys used in encryption are used in the reverse order.
Number of Rounds
More number of rounds provide more secure system.Number of rounds in the systems thus depend upon efficiency–security tradeoff.
9. DATA ENCRYPTION STANDARD
- It uses 16 round Feistel structure.
- The block size is 64-bit. DES has an effective key length of 56 bits, since 8 of the 64 bits of the key are not used by the encryption algorithm (function as check bits only).
- Round function
- Key schedule
- Any additional processing – Initial and final permutation
Initial and Final Permutation
Round Function
Key Generation
The round-key generator creates sixteen 48-bit keys out of a 56-bit cipher key.
DES Analysis
10. TRIPLE DES
There are two variants of Triple DES known as 3-key Triple DES (3TDES) and 2-key Triple DES (2TDES).3-KEY Triple DES
There are three different DES keys K1, K2 and K3. This means that the actual 3TDES key has length 3×56 = 168 bits.
- Encrypt the plaintext blocks using single DES with key K 1 .
- Now decrypt the output of step 1 using single DES with key K 2 .
- Finally, encrypt the output of step 2 using single DES with key K 3 .
- The output of step 3 is the ciphertext.
(2TDES) is identical to 3TDES except that K 3 is replaced by K 1 .
11. ADVANCED ENCRYPTION STANDARD
The Advanced Encryption Standard (AES) is found at least six time faster than triple DES.
Operation of AES
AES is an iterative rather than Feistel cipher.It is based on ‘substitution–permutation network’.
AES performs all its computations on bytes rather than bits.
Hence, AES treats the 128 bits of a plaintext block as 16 bytes.
These 16 bytes are arranged in four columns and four rows for processing as a matrix.
The number of rounds in AES is variable and depends on the length of the key. AES uses
- 10 rounds for 128-bit keys
- 12 rounds for 192-bit keys
- 14 rounds for 256-bit keys
Encryption Process
Each round of AES encryption comprise of four sub-processes.
- Byte Substitution (SubBytes) The 16 input bytes are substituted by looking up a fixed table (S-box) given in design. The result is in a matrix of four rows and four columns.
- Shiftrows Each of the four rows of the matrix is shifted to the left and rotated to the right.
- MixColumns Each column of four bytes is transformed using a special mathematical function.
- Addroundkey The 16 bytes of the matrix are now considered as 128 bits and are XORed to the 128 bits of the round key.
The result is a new matrix consisting of the same 16 bytes but shifted with respect to each other.
The result is another new matrix consisting of 16 new bytes.
It should be noted that this step is not performed in the last round.
Decryption Process
The process of decryption of an AES ciphertext is similar to the encryption process in the reverse order.AES Analysis
12. MODES OF OPERATION
A block cipher processes the data blocks of fixed size.The long message is divided into a series of sequential message blocks, and the cipher operates on these blocks one at a time.
Electronic Code Book (ECB) Mode
Operation:- the block of plaintext is encrypted with the same key to produce the block of ciphertext.
The ECB mode is deterministic, that is, if plaintext block P1, P2,..., Pm are encrypted twice under the same key, the output ciphertext blocks will be the same.
Thus, the operation is analogous to the assignment of code words in a codebook, and hence gets an official name: Electronic Codebook mode of operation (ECB).
Cipher Block Chaining (CBC) Mode
CBC mode of operation provides message dependence for generating ciphertext and makes the system non-deterministic.
- Load the n-bit Initialization Vector (IV) in the top register.
- XOR the n-bit plaintext block with data value in top register.
- Encrypt the result of XOR operation with underlying block cipher with key K.
- Feed ciphertext block into top register and continue the operation till all plaintext blocks are processed.
- For decryption, IV data is XORed with first ciphertext block decrypted. The first ciphertext block is also fed into to register replacing IV for decrypting next ciphertext block.
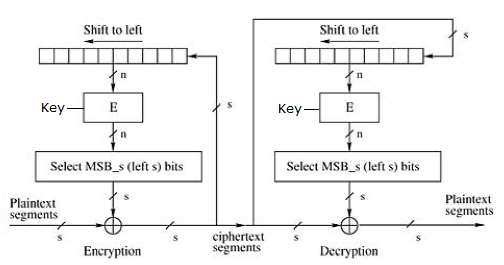
Cipher Feedback (CFB) Mode
In this mode, each ciphertext block gets ‘fed back’ into the encryption process in order to encrypt the next plaintext block.
- Load the IV in the top register.
- Encrypt the data value in top register with underlying block cipher with key K.
- Take only ‘s’ number of most significant bits (left bits) of output of encryption process and XOR them with ‘s’ bit plaintext message block to generate ciphertext block.
- Feed ciphertext block into top register by shifting already present data to the left
- continue the operation till all plaintext blocks are processed.
Similar steps are followed for decryption. Pre-decided IV is initially loaded at the start of decryption.
Apparently, CFB mode is converting a block cipher into a type of stream cipher.
The encryption algorithm is used as a key-stream generator to produce key-stream that is placed in the bottom register.
Output Feedback (OFB) Mode
It involves feeding the successive output blocks from the underlying block cipher back to it.
The OFB mode requires an IV as the initial random n-bit input block. The IV need not be secret.
Counter (CTR) Mode
13. PUBLIC KEY ENCRYPTION
Public Key Cryptography
The symmetric key was found to be non-practical due to challenges it faced for key management. The public key encryption:
- Different keys are used for encryption and decryption. This is a property which set this scheme different than symmetric encryption scheme.
- Each receiver possesses a unique decryption key, generally referred to as his private key.
- Receiver needs to publish an encryption key, referred to as his public key. Encryption algorithm is complex enough to prohibit attacker from deducing the plaintext from the ciphertext and the encryption (public) key.
There are three types of Public Key Encryption schemes.
RSA Cryptosystem
The system was invented by three scholars Ron Rivest, Adi Shamir, and Len Adleman and hence, it is termed as RSA cryptosystem.Generation of RSA Key Pair:
- Generate the RSA modulus (n)
- Select two large primes, p and q.
- Calculate n = p*q For strong unbreakable encryption, let n be a large number, typically a minimum of 512 bits.
- Find Derived Number (e)
- 1 < e < (p − 1)(q − 1)
- There must be no common factor for e and (p − 1)(q − 1) except for 1.(coprime).
- Form the public key The pair of numbers (n, e) form the RSA public key.
- Generate the private key Private Key d is calculated from p, q, and e.
Number d is the inverse of [e modulo (p − 1)(q – 1) ].
- Select p = 7 and q = 13
- n = pq = 7 x 13 = 91
- Select e = 5 there is no number that is common factor of 5 and (p − 1)(q − 1) = 6 × 12 = 72, except for 1.
- (n, e) = (91, 5) forms the public key
- the d calculated = 29 private keys is (91, 29)
ElGamal Cryptosystem
Elliptic Curve Cryptography (ECC)
RSA and ElGamal Schemes – A Comparison
14. DATA INTEGRITY
Threats to Data Integrity
The receiver must make sure that the message has come intact from the intended sender and is not modified inadvertently.15. HASH FUNCTIONS
A hash function is a mathematical function that converts a numerical input value into another compressed numerical value.The input to the hash function is of arbitrary length but output is always of fixed length.
Features of Hash Functions
- Fixed Length Output (Hash Value)
- Efficiency of Operation
Properties of Hash Functions
- Pre-Image Resistance it should be computationally hard to reverse a hash functionto find the input.
- Second Pre-Image Resistance it should be hard to find a different input with the same hash.
- Collision Resistance it should be hard to find two different inputs of any length that result in the same hash.
This property is also referred to as collision free hash function.
Design of Hashing Algorithms
The hashing is a mathematical function that operates on two fixed-size blocks of data to create a hash code.Hashing algorithm involves rounds of the hash function like a block cipher.
Each round takes an input of a fixed size, typically a combination of the most recent message block and the output of the last round.
This process is repeated for as many rounds as are required to hash the entire message.
Popular Hash Functions
- Message Digest (MD)
- The MD family comprises of hash functions MD2, MD4, MD5 and MD6.
- It is a 128-bit hash function.
- Secure Hash Function (SHA) SHA algorithms; SHA-0, SHA-1, SHA-2, and SHA-3.
- SHA-0, a 160-bit hash function
- SHA-1 is the most widely used of the existing SHA hash functions.
- SHA-2 family has four further SHA variants, SHA-224, SHA-256, SHA-384, and SHA-512 depending up on number of bits in their hash value.
- RIPEMD(RACE Integrity Primitives Evaluation Message Digest) The set includes RIPEND, RIPEMD-128, and RIPEMD-160. There also exist 256, and 320-bit versions of this algorithm.
- Whirlpool This is a 512-bit hash function.
Though from same family, there are structurally different.
Three versions of Whirlpool have been released; WHIRLPOOL-0, WHIRLPOOL-T, and WHIRLPOOL.
Applications of Hash Functions
16. MESSAGE AUTHENTICATION
Message Authentication Code (MAC) .................................................................................................... 64 Limitations of MAC ................................................................................................................................ 6517. DIGITAL SIGNATURE
Model of Digital Signature..................................................................................................................... 66 Importance of Digital Signature ............................................................................................................ 67 Encryption with Digital Signature .......................................................................................................... 6818. PUBLIC KEY INFRASTRUCTURE
Key Management .................................................................................................................................. 69 Public Key Infrastructure (PKI)............................................................................................................... 70 Digital Certificate .................................................................................................................................. 70 Certifying Authority (CA) ....................................................................................................................... 71 Hierarchy of CA ..................................................................................................................................... 7319. CRYPTOGRAPHY – BENEFITS AND DRAWBACKS
Cryptography – Benefits ........................................................................................................................ 75 Cryptography – Drawbacks ................................................................................................................... 75 Future of Cryptography ......................................................................................................................... 76SERIOUS CRYPTOGRAPHY : A Practical Introduction to Modern Encryption
Jean-Philippe AumassonChapter 1: Encryption
In symmetric encryption, the key used to decrypt is the same as the key used to encrypt.Plaintext --> Encryptor --> Ciphertest --> Decryptor --> Plaintext
Classic Ciphers
- 凱撒密碼（英語：Caesar cipher） 或稱凱撒加密、凱撒變換、變換加密，是一種最簡單且最廣為人知的加密技術。凱撒密碼是一種替換加密技術，明文中的所有字母都在字母表上向後（或向前）按照一個固定數目進行偏移後被替換成密文。例如，當偏移量是3的時候，所有的字母A將被替換成D，B變成E，以此類推。
明文字母表：ABCDEFGHIJKLMNOPQRSTUVWXYZ 密文字母表：DEFGHIJKLMNOPQRSTUVWXYZABC
For ex., if the key is DUH, letters in the plaintext are shifted with the following values repeatedly:
- 3 D is 3 letters after A
- 20 U is 20 letters after A
- 7 H is 7 letters after A
For example, suppose that
- the plaintext to be encrypted is: attackatdawn
- the keyword selected: LEMON
Plaintext: attackatdawn Key: LEMONLEMONLE Ciphertext: LXFOPVEFRNHR
How Ciphers Work
There are 2 main components:- permutation A function transform an item such that each item has an unique inverse
- a mode of operation An algorithm that uses a permutation to process messages of arbitrary size.
留言