Problem Solving with Algorithms and Data Structures using C++
Problem Solving with Algorithms and Data Structures using C++
By Brad Miller and David Ranum, Luther College, and Jan Pearce, Berea College
1. Introduction
1.1. Objectives
1.2. Getting Started
1.3. What Is Computer Science?
1.4. What Is Programming?
1.5. Why Study Data Structures and Abstract Data Types?
1.6. Why Study Algorithms?
1.7. Reviewing Basic C++
1.8. Getting Started with Data
1.9. Built-in Atomic Data Types
1.9.1. Numeric Data
1.9.2. Boolean Data
1.9.3. Character Data
1.9.4. Pointers
1.10. Collections
1.10.1. Arrays
1.10.2. Vectors
Vectors use a dynamically allocated array to store their elements, so they can change size, their size can change automatically.A new element can be inserted into or deleted from any part of a vector, and automatic reallocation for other existing items in the vector will be applied.
Vectors are homogeneous, so every element in the vector must be of the same type.
Vectors are a class that is available through a library called the Standard Template Library (STL), and one uses a < > notation to indicate the data type of the elements.
In order to use vectors, one needs to include the vector library:
#include <vector>Common C++ Vector operators and methods:
| operators/methods | Usage | Explanation |
|---|---|---|
| [ ] | myvector[i] | access value of element at index i |
| = | myvector[i]=value | assign value to element at index i |
| push_back() | myvect.push_back(item) | Appends item to the far end of the vector |
| pop_back() | myvect.pop_back() | Deletes last item (from far end) of the vector |
| insert() | myvect.insert(const_iterator position, item) | Inserts an item at index i |
| erase() | myvect.erase(const_iterator position) | Erases an element's position from index i |
| size() | myvect.size() | Returns the actual size used by elements |
| capacity() | myvect.capacity() | Returns the size of allocated storage capacity |
| reserve() | myvect.reserve(amount) | Request a change in capacity to amount |
1.10.3. Strings
There are actually two types of strings in C++ :- The C++ string or just string from the <string> library is the more modern type.
- The old style C-string which is essentially an array of char type.
char cppchar = 'a'; // char values use single quotes
string cppstring = "Hello World!"; // C++ strings use double quotes
char cstring[] = {"Hello World!"}; // C-string or char array uses double quotes
String Methods Provided in C++:
| [ ] | astring[i] | access value of character at index i |
| = | astring[i]=value | change value of character at index i |
| + | string1 + astring2 | concatenate strings |
| append | astring.append(string) | Append to string the end of the string |
| push_back | astring.push_back(char) | Appends a character to the end of the string |
| pop_back | astring.pop_back() | Deletes the last character from the end of the string |
| insert | astring.insert(i, string) | Inserts a string at a specific index |
| erase | astring.erase(i, j) | Erases an element from one index to another |
| find | astring.find(item) | Returns the index of the first occurrence of item |
| size | astring.size() | Returns the size of the string |
#include <iostream>
#include <string>
using namespace std;
int main(){
string mystring1 = "Hello";
string mystring2 = "World!";
string mystring3;
mystring3 = mystring1 + " " + mystring2;
cout << mystring3 << endl;
cout << mystring2 << " begins at ";
cout << mystring3.find(mystring2) << endl;
return 0;
}
$ ./test
Hello World!
World! begins at 6
Construct a string instance:
// string constructor
#include <iostream>
#include <string>
int main ()
{
std::string s0 ("Initial string");
// constructors used in the same order as described above:
std::string s1;
std::string s2 (s0);
std::string s3 (s0, 8, 3);
std::string s4 ("A character sequence", 6);
std::string s5 ("Another character sequence");
std::string s6 (10, 'x');
std::string s7a (10, 42);
std::string s7b (s0.begin(), s0.begin()+7);
std::cout << "s1: " << s1 << "\ns2: " << s2 << "\ns3: " << s3;
std::cout << "\ns4: " << s4 << "\ns5: " << s5 << "\ns6: " << s6;
std::cout << "\ns7a: " << s7a << "\ns7b: " << s7b << '\n';
return 0;
}
$ ./test
s1:
s2: Initial string
s3: str
s4: A char
s5: Another character sequence
s6: xxxxxxxxxx
s7a: **********
s7b: Initial
1.10.4. Hash Tables
A hash table is a collection of associated pairs of items where each pair consists of a key and a value.The key is used to uniquely identify the element and the mapped value is the content associated with the key.
Hash tables are often called the more general term map because the associated hash function “maps” the key to the value.
Both key and value can be of any type predefined or user-defined.
Each hash table has a hash function which given the key as input and returns the hash value as the output.
In C++ STL, the unordered_map implements the hash table, and the <unordered_map> library must be included.
Hash tables can be initialized with key-value pairs and key-value pairs can also be added later.
#include <iostream>
#include <unordered_map>
using namespace std;
int main()
{
// Declaring umap to be of <string, int> type
// key will be of string type and mapped value will
// be of int type
unordered_map<string, int> umap;
// inserting values by using [] operator
umap["GeeksforGeeks"] = 10;
umap["Practice"] = 20;
umap["Contribute"] = 30;
// Traversing an unordered map
for (auto x : umap)
cout << x.first << " = " << x.second << endl;
}
$ ./test
Contribute = 30
Practice = 20
GeeksforGeeks = 10
The foreach loop has two sections separated by a colon ( : ) instead of three separated by semicolons:
- The first section is a variable that will hold an element of the array.
- The second is the name of the array.
Important Hash Table Operators Provided in C++ :
| [ ] | mymap[k] | Returns the value associated with k, otherwise throws error |
| count | mymap.count(key) | Returns true if key is in mymap, false otherwise |
| erase | mymap.erase(key) | Removes the entry from mymap |
| begin | mymap.begin() | An iterator to the first element in mymap |
| end | mymap.end(key) | An iterator pointing to past-the-end element of mymap |
1.10.5. Unordered Sets
Set in C++ is an STL(standard template library) container.Sets are containers that store unique elements following a specific order.
Unordered sets are containers that store unique elements in no particular order, and which allow for fast retrieval of individual elements based on their value.
In an unordered_set, the value of an element is also its key, that identifies it uniquely.
Keys are immutable, therefore, the elements in an unordered_set cannot be modified once in the container - they can be inserted and removed, though.
Example code to detect if a specific char is in an unordered set:
#include <iostream>
#include <unordered_set>
using namespace std;
void checker(unordered_set<char> set, char letter){
if(set.find(letter) == set.end()){
cout << "letter " << letter << " is not in the set." << endl;
}
else{
cout << "letter " << letter << " is in the set." << endl;
}
}
int main(){
unordered_set<char> charSet = {'d', 'c', 'b', 'a'};
char letter = 'e';
checker(charSet, letter);
charSet.insert('e');
checker(charSet, letter);
return 0;
}
$ ./test
letter e is not in the set.
letter e is in the set.
Methods Provided by Sets in C++:
| union | set_union() | Returns a new set with all elements from both sets |
| intersection | set_intersection() | Returns a new set with only those elements common to both sets |
| difference | set_difference() | Returns a new set with all items from first set not in second |
| add | aset.insert(item) | Adds item to the set |
| remove | aset.erase(item) | Removes item from the set |
| clear | aset.clear() | Removes all elements from the set |
1.11. Defining C++ Functions
1.11.1. Parameter Passing: by Value versus by Reference
1.11.2. Arrays as Parameters in Functions
1.11.3. Function Overloading
1.12. Object-Oriented Programming in C++: Defining Classes
1.12.1. A Fraction Class
1.12.2. Abstraction and Encapsulation
1.12.3. Polymorphism
1.12.4. Self Check
1.13. Inheritance in C++
1.13.1. Logic Gates and Circuits
1.13.2. Building Circuits
1.14. Optional: Graphics in C++
1.14.1. Introduction to Turtles
1.14.2. Turtle & TurtleScreen
1.14.3. Geometry, Shapes, and Stamps
1.14.4. Advanced Features
1.15. Summary
1.16. Discussion Questions
1.17. Programming Exercises
1.18. Glossary
1.19. Matching
2. Analysis
2.1. Objectives
2.2. What Is Algorithm Analysis?
2.2.1. Some Needed Math Notation
2.2.2. Applying the Math Notation
2.3. Big-O Notation
2.4. An Anagram Detection Example
2.4.1. Solution 1: Checking Off
2.4.2. Solution 2: Sort and Compare
2.4.3. Solution 3: Brute Force
2.4.4. Solution 4: Count and Compare
2.5. Performance of C++ Data Collections
2.6. Analysis of Array and Vector Operators
2.7. Analysis of String Operators
2.8. Analysis of Hash Tables
2.9. Summary
2.10. Self Check
2.11. Discussion Questions
2.12. Programming Exercises
2.13. Glossary
2.14. Matching
3. Linear Structures
3.1. Objectives
3.2. What Are Linear Structures?
Vectors, stacks, queues, deques are examples of data collections whose items are ordered depending on how they are added or removed.
Collections such as these are often referred to as linear data structures.
Linear structures can be thought of as having two ends, one of the following is refered:
- the “left” and the “right”
- the “front” and the “rear”
- the “top” and the “bottom”
What distinguishes one linear structure from another is the way in which items are added and removed, in particular the location where these additions and removals occur.
1.14. Optional: Graphics in C++
1.14.1. Introduction to Turtles
1.14.2. Turtle & TurtleScreen
1.14.3. Geometry, Shapes, and Stamps
1.14.4. Advanced Features
1.15. Summary
1.16. Discussion Questions
1.17. Programming Exercises
1.18. Glossary
1.19. Matching
2. Analysis
2.1. Objectives
2.2. What Is Algorithm Analysis?
2.2.1. Some Needed Math Notation
2.2.2. Applying the Math Notation
2.3. Big-O Notation
2.4. An Anagram Detection Example
2.4.1. Solution 1: Checking Off
2.4.2. Solution 2: Sort and Compare
2.4.3. Solution 3: Brute Force
2.4.4. Solution 4: Count and Compare
2.5. Performance of C++ Data Collections
2.6. Analysis of Array and Vector Operators
2.7. Analysis of String Operators
2.8. Analysis of Hash Tables
2.9. Summary
2.10. Self Check
2.11. Discussion Questions
2.12. Programming Exercises
2.13. Glossary
2.14. Matching
3. Linear Structures
3.1. Objectives
3.2. What Are Linear Structures?
Vectors, stacks, queues, deques are examples of data collections whose items are ordered depending on how they are added or removed.
Collections such as these are often referred to as linear data structures.
Linear structures can be thought of as having two ends, one of the following is refered:
- the “left” and the “right”
- the “front” and the “rear”
- the “top” and the “bottom”
What distinguishes one linear structure from another is the way in which items are added and removed, in particular the location where these additions and removals occur.
3.3. What is a Stack?
LIFO, last-in first-out.3.4. The Stack Abstract Data Type
Stack in C++ STL with the example:
#include <iostream>
#include <stack>
using namespace std;
int main() {
stack<int> stack;
stack.push(21);
stack.push(22);
stack.push(24);
stack.push(25);
stack.pop();
stack.pop();
while (!stack.empty()) {
cout << ' ' << stack.top();
stack.pop();
}
}
The stack operations are given below.
- stack<datatype> creates a new stack that is empty. It needs no parameters and returns an empty stack. It can only contain a certain type of data. e.g. int, string etc.
- push(item) adds a new item to the top of the stack. It needs the item and returns nothing.
- pop() removes the top item from the stack. It needs no parameters and returns nothing. The stack is modified.
- top() returns the top item from the stack but does not remove it. It needs no parameters. The stack is not modified.
- empty() tests to see whether the stack is empty. It needs no parameters and returns a Boolean value.
- size() returns the number of items on the stack. It needs no parameters and returns an integer.
3.5. Using a Stack in C++
3.6. Simple Balanced Parentheses
Balanced parentheses means that each opening symbol has a corresponding closing symbol and the pairs of parentheses are properly nested.Solving the Balanced Parentheses Problem :
//simple program that checks for missing parantheses
#include <iostream>
#include <stack>
#include <string>
using namespace std;
// returns whether the parentheses in the input are balanced
bool parChecker(string symbolString) {
stack<string> s;
bool balanced = true;
int index = 0;
int str_len = symbolString.length();
while (index < str_len && balanced) {
string symbol;
symbol = symbolString[index];
if (symbol == "(") {
s.push(symbol); //pushes the open parentheses to the stack.
} else {
if (s.empty()) { //if there is no open parentheses in the stack,
//the closing parentheses just found makes the string unbalanced.
balanced = false;
} else { //if there is an open parentheses in the stack,
//the closing parentheses just found has a matching open parentheses.
s.pop();
}
}
index = index + 1;
}
if (balanced && s.empty()) { //if the string is balanced and there are no
//remaining open parentheses.
return true;
} else {
return false;
}
}
int main() {
cout << parChecker("((()))") << endl;
cout << parChecker("(()") << endl;
}
$ ./test
1
0
3.7. Balanced Symbols - A General Case
3.8. Converting Decimal Numbers to Binary Numbers
#include <iostream>
#include <stack>
#include <string>
using namespace std;
string divideBy2(int decNumber) {
//performs the conversion process.
stack<int> remstack;
while (decNumber > 0) {
//gets the remainder of division by 2
//and adds the remainder to a stack.
int rem = decNumber % 2;
remstack.push(rem);
decNumber = decNumber >> 1;
}
string binString = "";
while (!remstack.empty()) {
//adds the remainder numbers in the stack into a string.
binString.append(to_string(remstack.top()));
remstack.pop();
}
return binString;
}
int main() {
cout << divideBy2(42) << endl;
return 0;
}
$ ./test
101010
3.9. Infix, Prefix and Postfix Expressions
Each operator has a precedence level. Operators of higher precedence are used before operators of lower precedence.One way to write an expression that guarantees there will be no confusion with respect to the order of operations is to create what is called a fully parenthesized expression. This type of expression uses one pair of parentheses for each operator.
The type of notation is referred to as infix if the operator is in between the two operands that it is working on.
The position of the operator with respect to the operands create two expression formats, prefix and postfix.
Examples of Infix, Prefix, and Postfix:
| Infix Expression | Prefix Expression | Postfix Expression |
|---|---|---|
| A + B | + A B | A B + |
| A + B * C | + A * B C | A B C * + |
3.9.1. Conversion of Infix Expressions to Prefix and Postfix
3.9.2. General Infix-to-Postfix Conversion
3.9.3. Postfix Evaluation
3.10. What Is a Queue?
A queue is an ordered collection of items where the addition of new items happens at one end, called the “rear,” and the removal of existing items occurs at the other end, commonly called the “front.”This ordering principle is sometimes called FIFO, first-in first-out.
It is also known as “first-come first-served.”
3.11. The Queue Abstract Data Type
Elements are pushed into the "back" of the specific container and popped from its "front".The standard queue operations are given below.
- queue<dataType> queueName creates a new queue that is empty. It returns an empty queue.
- push(item) adds a new item to the rear of the queue. It needs the item and returns nothing.
- pop() removes the front item from the queue. It needs no parameters. The queue is modified.
- empty() tests to see whether the queue is empty. It needs no parameters and returns a Boolean value.
- size() returns the number of items in the queue. It needs no parameters and returns an integer.
- front() returns the first item in the queue without removing the item.
- back() returns the last item in the queue without removing the item.
3.12. Using a Queue in C++
#include <iostream>
#include <queue> // Using an STL queue
using namespace std;
int main() {
queue<int> newQueue;
newQueue.push(3);
newQueue.push(8);
newQueue.push(15);
cout << "Queue Empty? " << newQueue.empty() << endl;
cout << "Queue Size: " << newQueue.size() << endl;
cout << "Top Element of the Queue: " << newQueue.front() << endl;
newQueue.pop();
cout << "Top Element of the Queue: " << newQueue.front() << endl;
return 0;
}
$ ./test
Queue Empty? 0
Queue Size: 3
Top Element of the Queue: 3
Top Element of the Queue: 8
3.13. Simulation: Hot Potato
Consider the children’s game Hot Potato:- Children line up in a circle and pass an item from neighbor to neighbor as fast as they can
- When the action is stopped and the child who has the item (the potato) is removed from the circle
- Play continues until only one child is left.
Assume that
- the child holding the potato will be at the front of the queue.
- Upon passing the potato, the simulation will simply dequeue and then immediately enqueue that child
- After number of dequeue/enqueue operations, the child at the front will be removed permanently and another cycle will begin.
- This process will continue until only one name remains
//This program creates a simulation of hot potato.
#include <iostream>
#include <queue>
#include <string>
using namespace std;
string hotPotato(string nameArray[], int num) {
queue<string> simqueue;
int namelsLenght = nameArray->length();
for (int i = 0; i < namelsLenght; i++) {
//puts the entire array into a queue.
simqueue.push(nameArray[i]);
}
while (simqueue.size() > 1) { //loop continues until there is one remaining item.
for (int i = 0; i < num; i++) {
simqueue.push(simqueue.front());
simqueue.pop();
}
simqueue.pop();
}
return simqueue.front();
}
int main() {
string s[] = {"Bill", "David", "Susan", "Jane", "Kent", "Brad"};
cout << hotPotato(s, 7) << endl;
return 0;
}
3.14. Simulation: Printing Tasks
When students send printing tasks to the shared printer, the tasks are placed in a queue to be processed in a first-come first-served manner.3.14.1. Main Simulation Steps
- Create a queue of print tasks. The queue is empty to start.
- For each second (currentSecond)
- If there is a new print task created, add it to the queue with the currentSecond as the timestamp.
- The printer does one second of printing if necessary. It also subtracts one second from the time required for that task.
- If the printer's task has been completed, in other words the time required has reached zero, the printer is no longer busy.
- If the printer is not busy and if there is a task waiting
- Remove the next task from the print queue and assign it to the printer.
- compute the printing time(timeRemaining) needed for that task. pages * pagerate;
- Record the waiting time in the queue for that task to a vecor for final statistic processing.
- Based on the number of pages in the print task, figure out how much time will be required to complete the printing.
Each task will be given a timestamp upon its arrival.
3.14.2. C++ Implementation
- The Printer class
class Printer {
public:
Printer(int pagesPerMinute) {
pagerate = pagesPerMinute;
timeRemaining=0;
working = false;
}
void tick() {
//Performed once per second in the simulation.
if (working) { // If we're working on something...
timeRemaining--;// Subtract the remaining time.
if (timeRemaining <= 0)
working = false; // When finished, stop working.
}
}
bool busy() {
return working;
}
void startNext(Task newtask) {
currentTask=newtask;
timeRemaining=newtask.getPages()*60/pagerate;
working = true;
}
private:
int pagerate; // unit is pages per minute.
Task currentTask = {0};// Current task. default is a dummy value.
bool working; // Are we working on the current task?
int timeRemaining; // Time remaining, in "seconds".
};
- The constructor will allow the pages-per-minute setting to be initialized. How many pasge the printer can print out per minute.
The waitTime method can then be used to retrieve the amount of time spent in the queue before printing begins.
class Task {
public:
Task(int time) {
timestamp = time;
pages=(rand()%20) + 1;
}
int getStamp() {
return timestamp;
}
int getPages() {
return pages;
}
int waitTime(int currenttime) {
return (currenttime - timestamp);
}
private:
int timestamp;
int pages;
};
#include <queue>
#include <vector>
/*
numSeconds: totol time in seconde to run this simulation
*/
void simulation(int numSeconds, int pagesPerMinute) {
Printer labprinter(pagesPerMinute);
//The Queue ADT from the standard container library.
queue<Task> printQueue;
//A vector of wait-times for each task.
vector<int> waitingTimes;
//For every second in the simulation...
for (int i = 0; i < numSeconds; i++) {
//If there's a new printing task, add it to the queue.
if (newPrintTask()) {
Task task(i);//Create it...
printQueue.push(task);//Push it.
}
//If the printer is not busy and the queue is not empty:
if (!labprinter.busy() &&!printQueue.empty()) {
Task nextTask = printQueue.front(); // Assign a new task from the queue.
printQueue.pop(); // Remove it from the front
//Add the estimated wait time to our vector.
waitingTimes.push_back(nextTask.waitTime(i));
labprinter.startNext(nextTask);
}
//Process the current task.
labprinter.tick();
}
//Average out every wait time for the simulation.
float total=0;
for (int waitTime : waitingTimes)
total += waitTime;
cout << "Average Wait " << total/waitingTimes.size() << " secs " << printQueue.size() << " tasks remaining." << endl;
}
//Program that simulates printing task management.
#include <iostream>
#include <cstdlib>
int main() {
//Seed random number generator with the current time
//This ensures a unique random simulation every time it's ran.
srand(time(NULL));
for (int i=0; i < 10; i++) {
simulation(3600, 5);
}
return 0;
}
3.14.3. Discussion
3.15. What Is a Deque?
A deque, also known as a double-ended queue, is an ordered collection of items similar to the queue.What makes a deque different from queue:
- New items can be added and removed at either the front or the rear.
It is up to you to make consistent use of the addition and removal operations.
3.16. The Deque Abstract Data Type
The deque operations are given below.- deque<dataType> dequeName creates a new deque that is empty. It returns an empty deque.
- push_front(item) adds a new item to the front of the deque. It needs the item and returns nothing.
- push_back(item) adds a new item to the rear of the deque. It needs the item and returns nothing.
- pop_front() removes the front item from the deque. It needs no parameters. The deque is modified.
- pop_back() removes the rear item from the deque. It needs no parameters. The deque is modified.
- empty() tests to see whether the deque is empty. It needs no parameters and returns a boolean value.
- size() returns the number of items in the deque. It needs no parameters and returns an integer.
3.17. Using a Deque in C++
The Deque library from STL will provide a very nice set of methods upon which to build the details of the deque.Example code of a deque.
#include <iostream>
#include <deque>
#include <string>
using namespace std;
int main() {
deque<string> d;
cout << "Deque Empty? " << d.empty() << endl;
d.push_back("Zebra");
cout << "Deque Empty? " << d.empty() << endl;
d.push_front("Turtle"); //pushes to the front of the deque.
d.push_front("Panda");
d.push_back("Catfish"); //pushes to the back of the deque.
d.push_back("Giraffe");
cout << "Deque Size: " << d.size() << endl;
cout << "Item at the front: " << d.front() << endl;
cout << "Item at the back: " << d.back() << endl;
cout << endl << "Items in the Deque: " << endl;
int dsize = d.size();
for(int i = 0; i < dsize; i++){
//prints each item in the deque.
cout << d.at(i) << " ";
}
cout << endl;
d.pop_back();
d.pop_front();
cout << endl << "Item at the front: " << d.front() << endl;
cout << "Itm at the back: " << d.back() << endl;
cout << "Deque Size: " << d.size() << endl;
int dsize2 = d.size();
cout << endl << dsize2 << " Items in the Deque: " << endl;
for(int i = 0; i < dsize2; i++)
//prints each item in the deque.
cout << i << ":" << d.at(i) << "\n";
return 0;
}
$ ./test
Deque Empty? 1
Deque Empty? 0
Deque Size: 5
Item at the front: Panda
Item at the back: Giraffe
Items in the Deque:
Panda Turtle Zebra Catfish Giraffe
Item at the front: Turtle
Itm at the back: Catfish
Deque Size: 3
3 Items in the Deque:
0:Turtle
1:Zebra
2:Catfish
3.18. Palindrome-Checker
Palindrome「迴文」。中文當中是指倒正著念和反著念都相同的句子,前後對稱,例如「上海自來水來自海上」。英文當中是指正著看和反著看都相同的單字,例如「 madam 」。判斷迴文: 左端右端同步往中央移動,逐一比對字元。如果字串長度為奇數,那麼不必檢查中央字元。
The solution to this problem will use a deque to store the characters of the string.
The front of the deque will hold the first character of the string and the rear of the deque will hold the last character.
Program that detects palindromes.
#include <deque>
#include <iostream>
#include <string>
using namespace std;
bool palchecker(string aString) {
deque<char> chardeque;
int strLen = aString.length();
for (int i = 0; i < strLen; i++) {
//pushes each char in the string to the deque.
chardeque.push_back(aString[i]);
}
bool stillEqual = true;
while (chardeque.size() > 1 && stillEqual) {
char first = chardeque.front();
chardeque.pop_front();
char last = chardeque.back();
chardeque.pop_back();
if (first != last) { //if the two opposite positions of the
//word is not the same, then it is not
//a palindrome.
stillEqual = false;
}
}
return stillEqual;
}
int main() {
cout << palchecker("lsdkjfskf") << endl;
cout << palchecker("radar") << endl;
}
$ ./test
0
1
3.19. Summary
3.20. Discussion Questions
3.21. Programming Exercises
3.22. Glossary
3.23. Matching
4. Linear Linked Structures
4.1. Objectives
4.2. What Are Linked Structures?
4.3. Implementing an Unordered Linked List
A linked list is a linear collection of data elements, each element is stored in a node which points to the next node.
4.4. The Node Class
4.5. The Unordered Linked List Class
The unordered linked list will be built from a collection of nodes, each linked to the next by explicit pointers.the UnorderedList class must maintain a reference to the first node. A C++ implementation,
#include <iostream>
using namespace std;
//creates a node class
class Node {
//defines data, and next as a pointer.
private:
int data; //data in the beginning node
Node *next; //pointer to the next node
public:
Node(int initdata) {
data = initdata; //the initialized data is set as the head
next = NULL; //the next node is set as NULL, as there is no next node yet.
}
int getData() { //function that return data of a given node.
return data;
}
Node *getNext() { // pointer that gets the next node
return next;
}
void setData(int newData) { // sets data in node
data = newData;
}
void setNext(Node *newnext) {
next = newnext;
}
};
// creates unorderedlist that points to the head of the linked list
class UnorderedList {
public:
Node *head;
UnorderedList() { // makes the head node equal to null
head = NULL;
}
bool isEmpty() { // the head node is empty if it is null
return head == NULL;
}
void add(int item) { //cerates a "temp" pointer that adds the new node to the head of the list
Node *temp = new Node(item);
temp->setNext(head);
head = temp;
}
int size() { //cereates a "current" pointer that iterates through the list until it reaches null
Node *current = head;
int count = 0;
while (current != NULL) {
count++;
current = current->getNext();
}
return count;
}
// creates "current" pointer that iterates through the list
// untli it finds the item being searched for, and returns a boolean value
bool search(int item) {
Node *current = head;
while (current != NULL) {
if (current->getData() == item) {
return true;
} else {
current = current->getNext();
}
}
return false;
}
// uses current and previous pointer to iterate through the lists
// finds the items that is searched for, and removes it
void remove(int item) {
Node *current = head;
Node *previous = NULL;
bool found = false;
while (!found) {
if (current->getData() == item) {
found = true;
} else {
previous = current;
current = current->getNext();
}
}
if (previous == NULL) {
head = current->getNext();
} else {
previous->setNext(current->getNext());
}
}
friend ostream& operator<<(ostream& os, const UnorderedList& ol);
};
ostream& operator<<(ostream& os, const UnorderedList& ol) {
Node *current = ol.head;
while (current != NULL) {
os<<current->getData()<<endl;
current = current->getNext();
}
return os;
}
int main() {
UnorderedList mylist;
mylist.add(31);
mylist.add(77);
mylist.add(17);
mylist.add(93);
mylist.add(26);
mylist.add(54);
cout<<"SIZE: "<<mylist.size()<<endl;
cout<<"contains 93?\t"<<mylist.search(93)<<endl;
cout<<"contains 100?\t"<<mylist.search(100)<<endl<<endl;
mylist.add(100);
cout<<"contains 100?\t"<<mylist.search(100)<<endl<<endl;
cout<<"SIZE: "<<mylist.size()<<endl;
mylist.remove(54);
cout<<"SIZE: "<<mylist.size()<<endl;
mylist.remove(93);
cout<<"SIZE: "<<mylist.size()<<endl;
mylist.remove(31);
cout<<"SIZE: "<<mylist.size()<<endl;
mylist.search(93);
cout<<"MY LIST: "<<endl<<mylist;
return 0;
}
$ ./test
SIZE: 6
contains 93? 1
contains 100? 0
contains 100? 1
SIZE: 7
SIZE: 6
SIZE: 5
SIZE: 4
MY LIST:
100
26
17
77
4.6. Implementing an Ordered Linked List
// similar to unordered lists except it orders the data
#include <iostream>
using namespace std;
class Node {
private:
int data;
Node *next;
public:
Node(int initdata) {
data = initdata; //the nodes data.
next = NULL; //next will become a pointer to another Node object.
}
int getData() {
//returns the data of the Node.
return data;
}
Node *getNext() {
//returns the next Node in the linked list.
return next;
}
void setData(int newData) {
//Changes the data of the Node.
data = newData;
}
void setNext(Node *newnext) {
//assigns the next item in the linked list.
next = newnext;
}
};
class OrderedList {
public:
Node *head; //The first Node of the linked list.
OrderedList() {
head = NULL;
}
bool search(int item) {
//finds a Node that contains item in the linked list.
Node *current = head;
bool found = false;
bool stop = false;
while (current != NULL && !found && !stop) {
//iterates through the entire list until item is found.
if (current->getData() == item) {
found = true;
} else {
if (current->getData() > item) {
stop = true;
} else {
current = current->getNext();
}
}
}
return found;
}
void add(int item) {
if (head == NULL) {
Node *newNode = new Node(item);
head = newNode;
} else {
Node *current = head;
Node *previous = NULL;
bool stop = false;
while (current != NULL && !stop) {
if (current->getData() > item) { //if the data of the current Node is greater than item:
stop = true;
} else {
previous = current;
current = current->getNext();
}
}
Node *temp = new Node(item);
if (previous == NULL) {
//sets the current head as temp's next item,
//sets temp as the new head.
temp->setNext(head);
head = temp;
} else {
//sets the current Node as temp's next Node,
//sets temp to previous's next Node.
temp->setNext(current);
previous->setNext(temp);
}
}
}
bool isEmpty() {
//Returns true if the head is NULL.
return head == NULL;
}
int size() {
//returns the length of the linked list.
Node *current = head;
int count = 0;
while (current != NULL) {
count++;
current = current->getNext();
}
return count;
}
friend ostream& operator<<(ostream& os, const OrderedList& ol);
};
ostream& operator<<(ostream& os, const OrderedList& ol) {
//operator for printing the data of every Node in the list.
Node *current = ol.head;
while (current != NULL) {
os<<current->getData()<<endl;
current = current->getNext();
}
return os;
}
int main() {
OrderedList mylist;
mylist.add(31);
mylist.add(77);
mylist.add(17);
mylist.add(93);
mylist.add(26);
mylist.add(54);
cout<<"SIZE: "<<mylist.size()<<endl;
cout<<"contains 93?\t"<<mylist.search(93)<<endl;
cout<<"contains 100?\t"<<mylist.search(100)<<endl<<endl;
cout<<"MY LIST: "<<endl<<mylist;
return 0;
}
$ ./test
SIZE: 6
contains 93? 1
contains 100? 0
MY LIST:
17
26
31
54
77
93
4.6.1. Analysis of Linked Lists
4.7. The Ordered List Abstract Data Type
The structure of an ordered list is a collection of items where each item holds a relative position that is based upon some underlying characteristic of the item.
4.7.1. Forward lists
Forward lists are implemented as singly-linked lists.Forward lists use links that connect one element to another. For this reason you cannot directly access an element in a forward list without iterating through each element that comes before that element.
4.7.2. Lists
Lists are implemented as doubly-linked-lists.A list holds a link to the previous element and the next element.
5. Recursion
5.1. Objectives
5.2. What Is Recursion?
Recursion is a method of solving problems that involves breaking a problem down into smaller and smaller subproblems until you get to a small enough problem that it can be solved trivially.Recursion involves a function calling itself.
5.3. Calculating the Sum of a Vector of Numbers
#include <iostream>
#include <vector>
using namespace std;
int iterate_sum(int nums[]){
int theSum = 0;
for (int i = 0; i < 5; i++){
theSum += nums[i];
}
return theSum;
}
int dynamic_sum(vector<int> numVect){
if (numVect.size() <= 1){
return numVect[0];
}
else {
vector<int> slice(numVect.begin() + 1, numVect.begin()+numVect.size());
return numVect[0] + dynamic_sum(slice); //function makes a recursive call to itself.
}
}
int dynamic_sum(int nums[], int len){
if (len <= 1){
return nums[0];
}
else {
len--;
return nums[0] + dynamic_sum(nums + 1, len); //function makes a recursive call to itself.
}
}
int main() {
int nums[5] = {1, 3, 5, 7, 9};
int len = (sizeof(nums) / sizeof(nums[0]));
cout << "array's len: " << len << endl;
cout << "iterated sum(array): " << iterate_sum(nums) << endl;
vector<int> numVect(nums, nums + len); //Initializes vector with same items as nums.
cout << "dynamic sum(vector): " << dynamic_sum(numVect) << endl;
cout << "dynamic sum(array): " << dynamic_sum(nums, len) << endl;
return 0;
}
5.4. The Three Laws of Recursion
All recursive algorithms must obey three important laws:- A recursive algorithm must have a base case.
- A recursive algorithm must change its state and move toward the base case.
- A recursive algorithm must call itself, recursively.
5.5. Converting an Integer to a String in Any Base
The recursive formulation of the problem is very elegant.the overall algorithm will involve three components:
- Reduce the original number to a series of single-digit numbers.
- Convert the single digit-number to a string using a lookup.
- Concatenate the single-digit strings together to form the final result.
#include <iostream>
#include <string>
using namespace std;
string convertString = "0123456789ABCDEF"; // base table
string toStr(int n, int base) {
if (n < base) {
return string(1, convertString[n]); // lookup table to converts char to string, and returns it
} else {
return toStr(n/base, base) + convertString[n%base]; // function makes a recursive call to itself.
}
}
int main() {
cout << toStr(1453, 16) << endl;
}
5.6. Stack: Iteration Instead of Recursion
#include <iostream>
#include <string>
#include <stack>
using namespace std;
stack<char> rStack;
string convertString = "0123456789ABCDEF";
string toStr(int n, int base) {
while (n > 0) {
if (n < base) {
rStack.push(convertString[n]); //pushes the last string n to the stack
} else {
rStack.push(convertString[n % base]); //pushes string n modulo base to the stack.
}
n = n/base;
}
// combine results from the stack
string res;
while (!rStack.empty()) {
res = res + (string(1, rStack.top()));
rStack.pop();
}
return res;
}
int main() {
cout << toStr(1453, 16);
}
5.7. Introduction: Visualizing Recursion
5.8. Sierpinski Triangle
5.9. Complex Recursive Problems
some problems that are really difficult to solve using an iterative programming style but are very elegant and easy to solve using recursion.5.10. Tower of Hanoi
河內塔是根據一個傳說形成的數學問題: 有三根杆子A,B,C。A杆上有 N 個 穿孔圓盤,盤的尺寸由下到上依次變小。要求按下列規則將所有圓盤移至 C 杆:
- 每次只能移動一個圓盤
- 大盤不能疊在小盤上面
- 3个圆盘的河內塔的移动
- 4个圆盘的河內塔的移动
假设有 A、B、C 三个塔,A 塔有 N 塊盤,目标是把这些盤全部移到 C 塔。
- Move a tower of height-1 to an intermediate pole B, using the final pole C.
- Move the remaining disk to the final pole C,
- Move the tower of height-1 from the intermediate pole B to the final pole using the original pole A.
5.11. Exploring a Maze
5.12. Dynamic Programming
5.13. Summary
5.14. Self-check
5.15. Discussion Questions
5.16. Programming Exercises
5.17. Glossary
5.18. Matching
6. Searching and Hashing
6.1. Objectives
6.2. Searching
Searching is the algorithmic process of finding a particular item in a collection of items.A find function can be created for C++ arrays by passing in the array, the size of the array, and the value to search for as arguments.
#include <iostream>
using namespace std;
bool isIn(int alist[], int size, int value) {
for (unsigned i=0; i<size; i++) {
if (alist[i] == value) {
return true;
}
}
return false;
}
int main() {
int myarr[] = {3, 5, 2, 4, 1};
cout<<isIn(myarr, 5, 15)<<endl;
cout<<isIn(myarr, 5, 3)<<endl;
return 0;
}
$ ./test
0
1
6.3. The Sequential Search
#include <iostream>
#include <vector>
using namespace std;
// Checks to see if item is in a vector
// retruns true or false (1 or 0)
//using sequential Search
bool sequentialSearch(vector<int> avector, int item) {
unsigned int pos = 0;
bool found = false;
while (pos < avector.size() && !found) {
if (avector[pos] == item) {
found = true;
} else {
pos++;
}
}
return found;
}
int main() {
// Vector initialized using an array
int arr[] = {1, 2, 32, 8, 17, 19, 42, 13, 0};
vector<int> testvector(arr,arr+9);
cout << testvector.size() << endl;
for (vector<int>::iterator it = testvector.begin(); it != testvector.end(); ++it)
std::cout << ' ' << *it;
std::cout << '\n';
cout << sequentialSearch(testvector, 3) << endl;
cout << sequentialSearch(testvector, 13) << endl;
return 0;
}
6.3.1. Analysis of Sequential Search
6.4. The Binary Search
It is possible to take greater advantage of the ordered vector .A binary search will start by examining the middle item.
- If that item is the one we are searching for, we are done.
- If it is not the correct item, we can use the ordered nature of the vector to eliminate half of the remaining items. If the item we are searching for is greater than the middle item, the item, if it is in the vector, must be in the upper half.
#include <iostream>
using namespace std;
//retruns true or false (1 or 0)
//using binary Search and
//uses start and end indices
bool binarySearch(int arr[], int item, int start, int end) {
if (end >= start) {
int mid = start + (end - start) / 2;
if (arr[mid] == item)
return true;
if (arr[mid] > item)
return binarySearch(arr, item, start, mid - 1);
else {
return binarySearch(arr, item, mid + 1, end);
}
}
return false;
}
bool binarySearchHelper(int arr[], int size, int item) {
return binarySearch(arr, item, 0, size);
}
int main(void) {
int arr[] = {0, 1, 2, 8, 13, 17, 19, 32, 42};
int arrLength = sizeof(arr) / sizeof(arr[0]);
cout << binarySearchHelper(arr, arrLength, 3) << endl;
cout << binarySearchHelper(arr, arrLength, 13) << endl;
return 0;
}
6.4.1. Analysis of Binary Search
O(logn).6.5. Hashing
A data structure that can be searched in O(1) by using hashing.A hash table is a collection of items which are stored.
Each position of the hash table, often called a slot, can hold an item and is named by an integer value.
The mapping between an item and the slot where that item belongs in the hash table is called the hash function. The hash function will take any item in the collection and return an integer in the range of slot names, between 0 and m-1.
6.5.1. Hash Functions
Assume that :- we have the set of integer items 54, 26, 93, 17, 77, and 31.
- A hash table with size 11, hash function is the “remainder method,” simply takes an item and divides it by the table size, returning the remainder as its hash value. hash(item) = item % 11
| Item | Hash Value |
|---|---|
| 54 | 10 |
| 26 | 4 |
| 93 | 5 |
| 17 | 6 |
| 77 | 0 |
| 31 | 9 |
- use the hash function to compute the slot name for the item
- check the hash table to see if it is present on the slot
6.5.2. Collision Resolution
When two or more items having the same hash value and would need to be in the same slot. This is referred to as a collision.This collision resolution process is referred to as open addressing in that it tries to find the next open slot or address in the hash table. By systematically visiting each slot one at a time, we are performing an open addressing technique called linear probing. For the last ex,
- Original hash table
- Add the item 44, a collision occurs Under linear probing, we look sequentially from the next, slot by slot, until we find an open position.
- Add the item 55, a collision occurs It must be placed in slot 2 since it is the next open position.
- Add the item 20, a collision occurs Since slot 9 is full, we begin to do linear probing.
In this case, we find slot 1.
We visit slots 10, 0, 1, and 2, and finally find an empty slot at position 3.
- the hash value is 9, and slot 9 is currently holding 31 WHICH IS NOT MATCHED
- do a sequential search starting at position 10, looking until either we find the item 20 or we find an empty slot.
A Cluster of Items for Slot 0, One way to reduce the clustering is to extend the linear probing so that it look at every third slot until we find one that is empty.
For ex., 44 will be added to the slot 3, The general name for this process of looking for another slot after a collision is rehashing.
An alternative method for handling the collision problem is to allow each slot to hold a reference to a collection (or chain) of items.
Chaining allows many items to exist at the same slot in the hash table.
When we want to search for an item, we use the hash function to generate the slot where it should reside. Since each slot holds a collection, we use a searching technique to decide whether the item is present.
6.5.3. Implementing the Map Abstract Data Type
The C++ std::map is an associative data type where you can store key–data pairs.The key is used to look up the associated data.
The keys in a map are all unique so that there is a one-to-one relationship between a key and a value.
template < class Key, // map::key_type
class T, // map::mapped_type
class Compare = less<Key>, // map::key_compare
class Alloc = allocator<pair<const Key,T> > // map::allocator_type
> class map;
Basics:
// constructing maps
#include <iostream>
#include <map>
using namespace std;
bool fncomp (char lhs, char rhs) {return lhs<rhs;}
struct classcomp {
bool operator() (const char& lhs, const char& rhs) const
{return lhs<rhs;}
};
int main ()
{
// declare container and iterator
map<char,int> map1;
map<char,int>::iterator iter;
map<char,int>::reverse_iterator iter_r;
// insert element
map1.insert(pair<char,int>('a', 10));
map1['b']=30;
map1['c']=50;
map1['d']=70;
//traversal
for(iter = map1.begin(); iter != map1.end(); iter++)
cout << iter->first << ":" << iter->second << " ";
cout << endl;
for(iter_r = map1.rbegin(); iter_r != map1.rend(); iter_r++)
cout << iter_r->first << ":" << iter_r->second << " ";
cout << endl;
//find and erase the element
iter = map1.find('b');
if ( iter != map1.end() ){
cout << "Find, the value is "<< iter->second << ". Delete it." << endl;
// erase the element
map1.erase(iter);
} else
cout << "Do not Find" << endl;
map<char,int> map2 (map1.begin(),map1.end());
for(iter = map1.begin(); iter != map1.end(); iter++)
cout << iter->first << ":" << iter->second << " ";
cout << endl;
map<char,int> map3 (map2);
map<char,int,classcomp> map4; // class as Compare
bool(*fn_pt)(char,char) = fncomp;
map<char,int,bool(*)(char,char)> fifth (fn_pt); // function pointer as Compare
return 0;
}
$ ./test
a:10 b:30 c:50 d:70
d:70 c:50 b:30 a:10
Find, the value is 30. Delete it.
a:10 c:50 d:70
One of the great benefits of a map is the fact that given a key, we can look up the associated data value very quickly. The particular map can be implemented like this HashTable:
#include <iostream>
#include <string>
using namespace std;
class HashTable{
public:
static const int size=11; // initial size of hash table is prime to help with collision resolution
int slots[size]; // list to hold key items
string data[size]; // list to hold data values
int hashfunction(int key) { // implements remainder method
return key%size;
}
// Computes original hashvalue, and if slot is
// not empty iterates until empty slot is found
int rehash(int oldhash) {
return (oldhash+1)%size;
}
// Function that assumes there will eventually be
// an empty slot unless the key is alread present in the slot
void put(int key, string val){
int hashvalue = hashfunction(key);
int count = 0;
if (data[hashvalue]=="") {
slots[hashvalue] = key;
data[hashvalue] = val;
} else {
if (slots[hashvalue] == key) {
data[hashvalue] = val;
} else {
int nextslot = rehash(hashvalue);
while (data[nextslot]!="" && slots[nextslot] != key) {
nextslot = rehash(nextslot);
count++;
if (count>size) {
cout<<"TABLE FULL"<<endl;
return;
}
}
if (data[nextslot]=="") {
slots[nextslot]=key;
data[nextslot]=val;
} else {
data[nextslot] = val;
}
}
}
}
// computes the initial hash value
// if value is not in the initial slot, uses
// rehash to locate the next position
string get(int key) {
int startslot = hashfunction(key);
string val;
bool stop=false;
bool found=false;
int position = startslot;
while(data[position]!="" && !found && !stop) {
if (slots[position]==key) {
found = true;
val = data[position];
} else {
position=rehash(position);
if (position==startslot) {
stop=true;
}
}
}
return val;
}
friend ostream& operator<<(ostream& stream, HashTable& hash);
};
ostream& operator<<(ostream& stream, HashTable& hash) {
for (int i=0; i<hash.size; i++) {
stream<<hash.slots[i]<<": "<<hash.data[i]<<endl;
}
return stream;
}
int main() {
HashTable h;
h.put(54, "cat");
h.put(26, "dog");
h.put(93, "lion");
h.put(17, "tiger");
h.put(77, "bird");
h.put(31, "cow");
h.put(44, "goat");
h.put(55, "pig");
h.put(20, "chicken");
cout << h <<endl;
h.put(20,"chicken");
h.put(17,"tiger");
h.put(20,"duck");
cout << h.get(20)<<endl;
cout << h.get(99)<<endl;
return 0;
}
$ ./test
77: bird
44: goat
55: pig
20: chicken
26: dog
93: lion
17: tiger
22036:
-1379190440:
31: cow
54: cat
duck
6.5.4. Analysis of Hashing
6.6. Self Check
6.7. Summary
6.8. Discussion Questions
6.9. Programming Exercises
6.10. Glossary
6.11. Matching
7. Sorting
7.1. Objectives
7.2. Sorting
Sorting is the process of placing elements from a collection in some kind of order.There is a number of algorithms that were able to benefit from having a sorted list.
7.3. The Bubble Sort
The bubble sort makes multiple passes through an array.- It compares adjacent items one by one and exchanges those that are out of order.
- Each pass places the next largest value in its proper place.
For ex., the 1st pass in the following move the largest number to the correct position:
#include <iostream>
#include <vector>
using namespace std;
//function goes through list sorting adjacent values as it bubbles
//the largest value to the top.
void bubbleSort(vector<int> &avector) { //the vector for bubble sort
for (int passnum = avector.size()-1; passnum > 0; passnum -= 1) {
for (int i = 0; i < passnum; i++) {
if (avector[i] > avector[i+1]) {
int temp = avector[i];
avector[i] = avector[i+1];
avector[i+1] = temp;
}
}
}
return ;
}
int main() {
// Vector initialized using a static array
static const int arr[] = {54,26,93,17,77,31,44,55,20};
vector<int> avector (arr, arr + sizeof(arr) / sizeof(arr[0]) );
for (unsigned int i = 0; i < avector.size(); i++) {
cout << avector[i] << " ";
}
cout << endl;
bubbleSort(avector);
for (unsigned int i = 0; i < avector.size(); i++) {
cout << avector[i] << " ";
}
cout << endl;
return 0;
}
$ ./test
54 26 93 17 77 31 44 55 20
17 20 26 31 44 54 55 77 93
Regardless of how the items are arranged in the initial array, n−1 passes will be made to sort an array of size n.A bubble sort is often considered the most inefficient sorting method.
7.4. The Selection Sort
A selection sort looks for the largest value in each pass, places it in the proper location, ending the pass. The selection sort improves on the bubble sort by making only one exchange for every pass.
#include <iostream>
#include <vector>
using namespace std;
//function that sorts through values in vector through selection sort
void selectionSort(vector<int> &avector) {
for (int fillslot = (avector.size() - 1); fillslot >= 0; fillslot--) {
int positionOfMax = 0;
for (int location = 1; location < fillslot + 1; location++) {
if (avector[location] > avector[positionOfMax]) {
positionOfMax = location;
}
}
int temp = avector[fillslot];
avector[fillslot] = avector[positionOfMax];
avector[positionOfMax] = temp;
}
return ;
}
int main() {
// Vector initialized using a static array
static const int arr[] = {54, 26, 93, 17, 77, 31, 44, 55, 20};
vector<int> avector (arr, arr + sizeof(arr) / sizeof(arr[0]) );
// print the vector
for (unsigned int i = 0; i < avector.size(); i++) {
cout << avector[i] << " ";
}
cout << endl;
// Call to the selectionSort function
selectionSort(avector);
// print the vector
for (unsigned int i = 0; i < avector.size(); i++) {
cout << avector[i] << " ";
}
cout << endl;
return 0;
}
7.5. The Insertion Sort
The insertion sort always maintains a sorted subvector in the lower positions of the vector. Each new item is then “inserted” back into the previous subvector such that the sorted subvector is one item larger.7.6. The Shell Sort
7.7. The Merge Sort
Merge sort is a recursive algorithm that continually:- splits a vector in half
- Once the two halves are sorted, the fundamental operation, called a merge, is performed.
#include <iostream>
#include <vector>
using namespace std;
//function that prints the vector
void printl(vector<int> avector) {
for (unsigned int i=0; i<avector.size(); i++) {
cout << avector[i] << " ";
}
cout << endl;
}
//function sorts using mergesort.
vector<int> mergeSort(vector<int> avector) {
if (avector.size()>1) {
cout<<"Splitting: ";
printl(avector);
int mid = avector.size()/2;
//C++ Equivalent to using Python Slices
vector<int> lefthalf(avector.begin(),avector.begin()+mid);
vector<int> righthalf(avector.begin()+mid,avector.begin()+avector.size());
lefthalf = mergeSort(lefthalf);
righthalf = mergeSort(righthalf);
cout<<"Merging: ";
printl(lefthalf);
printl(righthalf);
unsigned i = 0;
unsigned j = 0;
unsigned k = 0;
while (i < lefthalf.size() && j < righthalf.size()) {
if (lefthalf[i] < righthalf[j]) {
avector[k]=lefthalf[i];
i++;
} else {
avector[k] = righthalf[j];
j++;
}
k++;
}
while (i<lefthalf.size()) {
avector[k] = lefthalf[i];
i++;
k++;
}
while (j<righthalf.size()) {
avector[k]=righthalf[j];
j++;
k++;
}
cout<<"Merged: ";
printl(avector);
}
return avector;
}
int main() {
// Vector initialized using a static array
static const int arr[] = {54, 26, 93, 17, 77, 31, 44, 55, 20};
vector<int> avector (arr, arr + sizeof(arr) / sizeof(arr[0]) );
printl(mergeSort(avector));
return 0;
}
$ ./test
Splitting: 54 26 93 17 77 31 44 55 20
Splitting: 54 26 93 17
Splitting: 54 26
Merging: 54
26
Merged: 26 54
Splitting: 93 17
Merging: 93
17
Merged: 17 93
Merging: 26 54
17 93
Merged: 17 26 54 93
Splitting: 77 31 44 55 20
Splitting: 77 31
Merging: 77
31
Merged: 31 77
Splitting: 44 55 20
Splitting: 55 20
Merging: 55
20
Merged: 20 55
Merging: 44
20 55
Merged: 20 44 55
Merging: 31 77
20 44 55
Merged: 20 31 44 55 77
Merging: 17 26 54 93
20 31 44 55 77
Merged: 17 20 26 31 44 54 55 77 93
17 20 26 31 44 54 55 77 93
The merge operation which results in a vector of size n requires n operations. The result of this analysis is that: log(n) splits, each of which costs n for a total of n*log(n) operations.
Therefore, a merge sort is an O(n*log(n)) algorithm.
7.8. The Quick Sort
A quick sort first selects a value, which is called the pivot value.The role of the pivot value is to assist with splitting the list.
- Decide the pivot value There are many different ways to choose the pivot value, the simple way is to use the 1st as our first pivot value.
- Finding the Split Point Partitioning begins by locating two position markers — let’s call them leftmark and rightmark — at the beginning and end of the remaining items in the list.
- increment leftmark until we locate a value that is greater than the pivot value
- decrement rightmark until we find a value that is less than the pivot value
- exchange these two items
- Completing the Partition Process The pivot value can be exchanged with the contents of the split point and the pivot value is now in place.
The actual position where the pivot value belongs in the final sorted list, commonly called the split point, will be used to divide the list for subsequent calls to the quick sort.
The goal of the partition process is to move items that are on the wrong side with respect to the pivot value.
#include <iostream>
#include <vector>
using namespace std;
void printl(vector<int> avector) {
for (unsigned i=0; i<avector.size(); i++) {
cout<<avector[i]<<" ";
}
cout<<endl;
}
//function partitions vector depending on pivot value
int partition(vector<int> &avector, int first, int last) {
int pivotvalue = avector[first];
int rightmark = last;
int leftmark = first+1;
bool done = false;
while(! done){
while(leftmark<=rightmark && avector[leftmark]<=pivotvalue){
leftmark++;
}
while(rightmark>=leftmark && avector[rightmark]>=pivotvalue){
rightmark--;
}
if(rightmark<leftmark){
done = true;
}
else{
swap(avector[rightmark], avector[leftmark]);
}
}
swap(avector[rightmark], avector[first]);
return rightmark;
}
//recursive function that quicksorts through a given vector
void quickSort(vector<int> &avector, int first, int last) {
int splitpoint;
if (first<last) {
splitpoint = partition(avector,first,last);
quickSort(avector,first,splitpoint);
quickSort(avector,splitpoint+1,last);
}
}
int main() {
// Vector initialized using a static array
static const int arr[] = {54, 26, 93, 17, 77, 31, 44, 55, 20};
vector<int> avector (arr, arr + sizeof(arr) / sizeof(arr[0]) );
quickSort(avector,0,avector.size()-1);
printl(avector);
return 0;
}
std::swap() exchange values of two objects.
7.9. Self Check
7.10. Summary
7.11. Discussion Questions
7.12. Programming Exercises
7.13. Glossary
7.14. Matching
8. Trees and Tree Algorithms
8.1. Objectives
8.2. Examples of Trees
A tree data structure has a root, branches, and leaves.An example of tree is a simple web page written using HTML:
<html xmlns="http://www.w3.org/1999/xhtml" xml:lang="en" lang="en">
<head>
<meta http-equiv="Content-Type" content="text/html; charset=utf-8"/>
<title>simple</title>
</head>
<body>
<h1>A simple web page</h1>
<ul>
<li>List item one</li>
<li>List item two</li>
</ul>
<h2>
<a href="http://www.cs.luther.edu">Luther CS </a>
</h2>
</body>
</html>
8.3. Vocabulary and Definitions
- Node
- Edge An edge connects two nodes to show that there is a relationship between them.
- Path A path is an ordered list of nodes that are connected by edges.
- Children
- Parent
- Sibling Nodes in the tree that are children of the same parent are said to be siblings.
- Subtree
- Leaf Node
- Level The level of a node n is the number of edges on the path from the root node to n.
- Height The height of a tree is equal to the maximum level of any node in the tree.
8.4. Nodes and References
The attributes left and right will become references to other instances of the BinaryTree class in this representation.
#include <iostream>
#include <cstdlib>
using namespace std;
//creates a binary tree, allows you to insert nodes
// and access those nodes.
class BinaryTree {
private:
char key;
BinaryTree *leftChild; // reference other instances of the binary tree the BinaryTree class
BinaryTree *rightChild; // reference other instances of the binary tree the BinaryTree class
public: //constructor function expects to get some kind of object to store in the root
BinaryTree(char rootObj){
this->key = rootObj;
this->leftChild = NULL;
this->rightChild = NULL;
}
void insertLeft(char newNode){ // Handles insertion if there is no left child simply adds a node to the tree.
if (this->leftChild == NULL){
this->leftChild = new BinaryTree(newNode);
}
else { // handles insertion if there is a left child pushes the existing child down one level in the tree.
BinaryTree *t = new BinaryTree(newNode);
t->leftChild = this->leftChild;
this->leftChild = t;
}
}
void insertRight(char newNode){
if (this->rightChild == NULL){
this->rightChild = new BinaryTree(newNode);
}
else {
BinaryTree *t = new BinaryTree(newNode);
t->rightChild = this->rightChild;
this->rightChild = t;
}
}
BinaryTree *getRightChild(){ // accessor method
return this->rightChild;
}
BinaryTree *getLeftChild(){ // accessor method
return this->leftChild;
}
void setRootVal(char obj){ // accessor method
this->key = obj;
}
char getRootVal(){ // accessor method
return this->key;
}
};
void free_tree(BinaryTree *root){
if ( root->getLeftChild() )
free_tree(root->getLeftChild());
if ( root->getRightChild() )
free_tree(root->getRightChild());
cout << "delete: " << root->getRootVal() << endl;
delete root;
}
int main() {
BinaryTree *r = new BinaryTree('a');
cout << "init a\n";
cout << r->getRootVal() << endl;
cout << r->getLeftChild() << endl;
cout << "insert b\n";
r->insertLeft('b');
cout << r->getLeftChild() << endl;
cout << r->getLeftChild()->getRootVal() << endl;
cout << "insert c\n";
r->insertRight('c');
cout << r->getRightChild() << endl;
cout << r->getRightChild()->getRootVal() << endl;
cout << "insert d\n";
r->getRightChild()->setRootVal('d');
cout << r->getRightChild()->getRootVal() << endl;
free_tree(r);
return 0;
}
$ ./test
init a
a
0
insert b
0x603000000040
b
insert c
0x603000000070
c
insert d
d
delete: b
delete: d
delete: a
8.5. Parse Tree
A parse tree or parsing tree or derivation tree or concrete syntax tree is an ordered, rooted tree that represents the syntactic structure of a string according to some context-free grammar.Parse Tree for ((7+3)∗(5−2)),
8.6. Tree Traversals
There are three commonly used patterns to visit all the nodes in a tree, the difference is when the node's value is examined:- preorder Node is examined before visiting its children.
void preorder(){
cout << this->key << endl;
if (this->leftChild){
this->leftChild->preorder();
}
if (this->rightChild){
this->rightChild->preorder();
}
}
void inorder(BinaryTree *tree){
if (tree != NULL){
inorder(tree->getLeftChild());
cout << tree->getRootVal();
inorder(tree->getRightChild());
}
}
void postorder(BinaryTree *tree){
if (tree != NULL){
postorder(tree->getLeftChild());
postorder(tree->getRightChild());
cout << tree->getRootVal() << endl;
}
}
For each node visited, push its children to the queue so that the the nodes in the queue is ordered according to the level.
void BinaryTree::Levelorder(){
std::queue<TreeNode*> q;
q.push(this->root); // 把root作為level-order traversal之起點
// 推進queue中
while (!q.empty()){ // 若queue不是空的, 表示還有node沒有visiting
TreeNode *current = q.front(); // 取出先進入queue的node
q.pop();
std::cout << current->str << " "; // 進行visiting
if (current->leftchild != NULL){ // 若leftchild有資料, 將其推進queue
q.push(current->leftchild);
}
if (current->rightchild != NULL){ // 若rightchild有資料, 將其推進queue
q.push(current->rightchild);
}
}
}
8.7. Priority Queues with Binary Heaps
In a priority queue the logical order of items inside a queue is determined by their priority:- the highest priority items are at the front of the queue
- the lowest priority items are at the back
A binary heap will allow us both enqueue and dequeue items in O(logn).
The binary heap has two common variations:
- the min heap in which the smallest key is always at the front, and
- the max heap in which the largest key value is always at the front.
8.8. Priority Queues with Binary Heaps Example
Using a min or max heap would allow us to construct a tree that the children are always larger or smaller than the parent, respectively.In the example in this section we will be using min heap structure.
- The smallest element will always be at the root
- When inserting new elements into the heap Add the node to be the right-most leave.
- When deleting an root item Remove the root and replace it with the right-most leaf.
Make sure every parent node is smaller then the child node which we want to insert.
If the inserted node is the smallest node in the tree it will bubble up to the root and push everything else lower into the heap.
By swaping it with the lesser of its children, then the structure will be correct agian.
- homework insertion process into priority queue
- homework deleting process from the priority queue Remove the root and put the right most leaf in its place and than rearange the heap back to the proper state
8.9. Binary Heap Operations
Heaps are commonly implemented with an array, any binary tree can be stored in an array. The node with index i :- The left child of the node is at index: 2*i + 1
- The left child of the node is at index: 2*i + 2
- The parent of the node is at index: (i-1)/2
- BinaryHeap() creates a new, empty, binary heap.
- insert(k) adds a new item to the heap.
- findMin() returns the item with the minimum key value, leaving item in the heap.
- delMin() returns the item with the minimum key value, removing the item from the heap.
- isEmpty() returns true if the heap is empty, false otherwise.
- size() returns the number of items in the heap.
- buildHeap(vector) builds a new heap from a vector of keys.
#include <iostream>
#include <vector>
using namespace std;
class BinHeap{
private:
vector<int> heapvector;
int currentSize;
public:
BinHeap(vector<int> heapvector){
this->heapvector = heapvector;
this->currentSize = 0;
}
void print(){
int i=0;
for ( i=0 ; i < heapvector.size(); i++ )
cout << heapvector[i] << " ";
cout << endl;
}
void upHeap(int i){
while ((i / 2) > 0){
if (this->heapvector[i] < this->heapvector[i/2]){ // compare with its parent
int tmp = this->heapvector[i/2];
this->heapvector[i/2] = this->heapvector[i];
this->heapvector[i] = tmp;
i = i/2;
} else
break;
}
}
void insert(int k){
this->heapvector.push_back(k);
this->currentSize = this->currentSize + 1;
this->upHeap(this->currentSize);
}
void downHeap(int i){
while ((i*2) <= this->currentSize){
int mc = this->minChild(i);
if (this->heapvector[i] > this->heapvector[mc]){
int tmp = this->heapvector[i];
this->heapvector[i] = this->heapvector[mc];
this->heapvector[mc] = tmp;
}
i = mc;
}
}
int minChild(int i){
if (((i*2)+1) > this->currentSize){
return i * 2;
}
else{
if (this->heapvector[i*2] < this->heapvector[(i*2)+1]){
return i * 2;
}
else{
return (i * 2) + 1;
}
}
}
int delMin(){
int retval = this->heapvector[1];
this->heapvector[1] = this->heapvector[this->currentSize];
this->currentSize = this->currentSize - 1;
this->heapvector.pop_back();
this->downHeap(1);
return retval;
}
// build an entire heap from a vector of keys.
void buildheap(vector<int> avector){
int i = avector.size() / 2;
this->currentSize = avector.size();
this->heapvector.insert(this->heapvector.end(), avector.begin(), avector.end());
while (i > 0){
this->downHeap(i);
i = i - 1;
}
}
bool isEmpty(){
if (this->heapvector.size()>0){
return false;
}
return true;
}
int findMin(){
return this->heapvector[1];
}
};
int main(){
vector<int> vec;
vec.push_back(0);
BinHeap *bh = new BinHeap(vec);
cout << "Begin: ";
bh->print();
bh->insert(5);
bh->insert(7);
bh->insert(3);
bh->insert(11);
cout << "After insertting...\n";
bh->print();
cout << bh->delMin() << " is deleted\n";
cout << bh->delMin() << " is deleted\n";
cout << bh->delMin() << " is deleted\n";
cout << bh->delMin() << " is deleted\n";
cout << "AFter deleting...\n";
bh->print();
return 0;
}
$ ./test
Begin: 0
After insertting...
0 3 7 5 11
3 is deleted
5 is deleted
7 is deleted
11 is deleted
AFter deleting...
0
8.10. Binary Heap Implementation
8.10.1. The Structure Property
8.10.2. The Heap Order Property
8.10.3. Heap Operations
8.11. Binary Search Trees
Binary search trees is another way to map from a key to a value.
8.12. Search Tree Operations
8.13. Search Tree Implementation
A binary search tree relies on the property that:- keys that are less than the parent are found in the left subtree
- keys that are greater than the parent are found in the right subtree
The following picture represents the nodes that exist after we have inserted the following keys in the order shown:
70, 31, 93, 94, 14, 23, 73.
If we want to delete a node which has 2 children, we need to find its successor which will preserve the binary search tree relationships for both of the existing left and right subtrees.
#include <iostream>
#include <cstdlib>
#include <cstddef>
#include <string>
using namespace std;
//The TreeNode class represents a node, or vertex, in a tree heirarchy.
class TreeNode{
public:
int key;
string payload;
TreeNode *leftChild;
TreeNode *rightChild;
TreeNode *parent;
// Using Optional parameters make it
// easy for us to create a TreeNode under several different circumstances.
TreeNode(int key, string val, TreeNode *parent = NULL, TreeNode *left = NULL, TreeNode *right = NULL){
this->key = key;
this->payload = val;
this->leftChild = left;
this->rightChild = right;
this->parent = parent;
}
// Returns a pointer to the left child of this node.
// If null, the child doesn't exist.
TreeNode *hasLeftChild(){
return this->leftChild;
}
//Returns a pointer to the right child of this node.
//If null, the child doesn't exist.
TreeNode *hasRightChild(){
return this->rightChild;
}
//Returns a boolean indicating if this node is the left child of its parent.
bool isLeftChild(){
return this->parent && this->parent->leftChild == this;
}
//Returns a boolean indicating if this node is the right child of its parent.
bool isRightChild(){
return this->parent && this->parent->rightChild == this;
}
//Returns a boolean indicating if this node is a root node (has no parent).
bool isRoot(){
return !this->parent;
}
//Returns a boolean indicating if this node has no children.
bool isLeaf(){
return !(this->rightChild || this->leftChild);
}
// Returns a boolean indicating if this node has children.
bool hasAnyChildren(){
return this->rightChild || this->leftChild;
}
//Returns a boolean indicating if this node has both children.
bool hasBothChildren(){
return this->rightChild && this->leftChild;
}
//Removes this node from the tree it exists in,
//making it the root node of its own tree.
void spliceOut(){
if (this->isLeaf()){
if (this->isLeftChild()){
this->parent->leftChild = NULL;
}
else{
this->parent->rightChild = NULL;
}
}
else if (this->hasAnyChildren()){
if (this->hasLeftChild()){
if (this->isLeftChild()){
this->parent->leftChild = this->leftChild;
}
else{
this->parent->rightChild = this->rightChild;
}
this->leftChild->parent = this->parent;
}
else{
if (this->isLeftChild()){
this->parent->leftChild = this->rightChild;
}
else{
this->parent->rightChild = this->rightChild;
}
this->rightChild->parent = this->parent;
}
}
}
// Uses same properties of binary search tree
// that cause an inorder traversal to print out the
// nodes in the tree from smallest to largest.
TreeNode *findSuccessor(){
TreeNode *succ = NULL;
if (this->hasRightChild()){
succ = this->rightChild->findMin();
}
else{
if (this->parent){
if (this->isLeftChild()){
succ = this->parent;
}
else{
this->parent->rightChild = NULL;
succ = this->parent->findSuccessor();
this->parent->rightChild = this;
}
}
}
return succ;
}
//Finds the leftmost node out of all of this node's children.
TreeNode *findMin(){
TreeNode *current = this;
while (current->hasLeftChild()){
current = current->leftChild;
}
return current;
}
//Sets the variables of this node. lc/rc are left child and right child.
void replaceNodeData(int key, string value, TreeNode *lc = NULL, TreeNode *rc = NULL){
this->key = key;
this->payload = value;
this->leftChild = lc;
this->rightChild = rc;
if (this->hasLeftChild()){
this->leftChild->parent = this;
}
if (this->hasRightChild()){
this->rightChild->parent = this;
}
}
};
class BinarySearchTree{
// that is the root of the binary search tree.
private:
TreeNode *root;
int size;
/* Search the binary tree comparing the new key to the key in the current node:
* If the new key is less than the current node, search the left subtree.
* If the new key is greater than the current node, search the right subtree.
* When there is no left (or right) child to search, we have found the position in the tree where the new node should be installed.
* To add a node to the tree:
Create a new TreeNode object and insert the object at the point discovered in the previous step.
*/
// this is all done recursively
void _put(int key, string val, TreeNode *currentNode){
if (key < currentNode->key){
if (currentNode->hasLeftChild()){
this->_put(key, val, currentNode->leftChild);
}
else{
currentNode->leftChild = new TreeNode(key, val, currentNode);
}
}
else{
if (currentNode->hasRightChild()){
this->_put(key, val, currentNode->rightChild);
}
else{
currentNode->rightChild = new TreeNode(key, val, currentNode);
}
}
}
// Uses the same search method as _put, and returns
// a TreeNode to get
TreeNode *_get(int key, TreeNode *currentNode){
if (!currentNode){
return NULL;
}
else if (currentNode->key == key){
return currentNode;
}
else if (key < currentNode->key){
return this->_get(key, currentNode->leftChild);
}
else{
return this->_get(key, currentNode->rightChild);
}
}
public:
BinarySearchTree(){
this->root = NULL;
this->size = 0;
}
int length(){
return this->size;
}
// Checks to see if the tree has a root,
// if there is not a root then it will create a new TreeNode
// and install it as the root of the tree.
// If a root node is already in place than it calls _put
// to search the tree
void put(int key, string val){
if (this->root){
this->_put(key, val, this->root);
}
else{
this->root = new TreeNode(key, val);
}
this->size = this->size + 1;
}
// prints string associated with key to console
string get(int key){
if (this->root){
TreeNode *res = this->_get(key, this->root);
if (res){
return res->payload;
}
else{
return 0;
}
}
else{
return 0;
}
}
// checks to make sure the key of the root matches the key that is to be deleted.
// In either case if the key is not found an error is raised.
// If the node is found and has no childeren it is deleted
// If the node has a single child, the child takes the place of the parent.
void del(int key){
if (this->size > 1){
TreeNode *nodeToRemove = this->_get(key, this->root);
if (nodeToRemove){
this->remove(nodeToRemove);
this->size = this->size - 1;
}
else{
cerr << "Error, key not in tree" << endl;
}
}
else if (this->size == 1 && this->root->key == key){
this->root = NULL;
this->size = this->size - 1;
}
else{
cerr << "Error, key not in tree" << endl;
}
}
void remove(TreeNode *currentNode){
if (currentNode->isLeaf()){ //leaf
if (currentNode == currentNode->parent->leftChild){
currentNode->parent->leftChild = NULL;
}
else{
currentNode->parent->rightChild = NULL;
}
}
else if (currentNode->hasBothChildren()){ //interior
TreeNode *succ = currentNode->findSuccessor();
succ->spliceOut();
currentNode->key = succ->key;
currentNode->payload = succ->payload;
}
else{ // this node has one child
if (currentNode->hasLeftChild()){
if (currentNode->isLeftChild()){
currentNode->leftChild->parent = currentNode->parent;
currentNode->parent->leftChild = currentNode->leftChild;
}
else if (currentNode->isRightChild()){
currentNode->leftChild->parent = currentNode->parent;
currentNode->parent->rightChild = currentNode->leftChild;
}
else{
currentNode->replaceNodeData(currentNode->leftChild->key,
currentNode->leftChild->payload,
currentNode->leftChild->leftChild,
currentNode->leftChild->rightChild);
}
}
else{
if (currentNode->isLeftChild()){
currentNode->rightChild->parent = currentNode->parent;
currentNode->parent->leftChild = currentNode->rightChild;
}
else if (currentNode->isRightChild()){
currentNode->rightChild->parent = currentNode->parent;
currentNode->parent->rightChild = currentNode->rightChild;
}
else{
currentNode->replaceNodeData(currentNode->rightChild->key,
currentNode->rightChild->payload,
currentNode->rightChild->leftChild,
currentNode->rightChild->rightChild);
}
}
}
}
};
int main(){
BinarySearchTree *mytree = new BinarySearchTree();
mytree->put(3, "C");
mytree->put(4, "D");
mytree->put(6, "F");
mytree->put(2, "B");
cout << mytree->get(6) << endl;
cout << mytree->get(2) << endl;
return 0;
}
./test
F
B
8.14. Search Tree Analysis
The answer to this question depends on how the keys are added to the tree.It is possible to construct a search tree that has height n simply by inserting the keys in sorted order !
In a balanced binary tree, the worst-case performance of put is O(log2n).
8.15. Balanced Binary Search Trees
The performance of the binary search tree can degraded when the tree becomes unbalanced.An AVL tree, named for its inventors: G.M. Adelson-Velskii and E.M. Landis, automatically makes sure that the tree remains balanced at all times.
To implement our AVL tree we need to keep track of a balance factor for each node in the tree.
balanceFactor = height(leftSubTree) − height(rightSubTree)Once the balance factor of a node in a tree is outside this range we will need to have a procedure to bring the tree back into balance.
8.16. AVL Tree Performance
8.17. AVL Tree Implementation
- All new keys are inserted into the tree as leaf nodes
- Once the new leaf is added we must update the balance factor of its parent.
- If the new node is a right child the balance factor of the parent will be reduced by one.
- If the new node is a left child then the balance factor of the parent will be increased by one.
- until the balance factor of the parent has been adjusted to zero. Once a subtree has a balance factor of zero, then the balance of its ancestor nodes does not change.
- until to the root of the tree.
int updateBalance(TreeNode *node){
if (node->balanceFactor > 1 || node->balanceFactor < -1){
this->rebalance(node);
return 0;
}
if (node->parent != NULL){
if (node->isLeftChild()){
node->parent->balanceFactor += 1;
}
else if (node->isRightChild()){
node->parent->balanceFactor -= 1;
}
if (node->parent->balanceFactor != 0){
this->updateBalance(node->parent);
}
}
}
In order to bring an AVL Tree back into balance we will perform one or more rotations on the tree.
- Transforming an Unbalanced Tree Using a Left Rotation
- Transforming an Unbalanced Tree Using a Right Rotation
void rotateLeft(TreeNode *rotRoot){
TreeNode *newRoot = rotRoot->rightChild;
rotRoot->rightChild = newRoot->leftChild;
if (newRoot->leftChild != NULL){
newRoot->leftChild->parent = rotRoot;
}
newRoot->parent = rotRoot->parent;
if (rotRoot->isRoot()){
this->root = newRoot;
}
else{
if (rotRoot->isLeftChild()){
rotRoot->parent->leftChild = newRoot;
}
else{
rotRoot->parent->rightChild = newRoot;
}
}
newRoot->leftChild = rotRoot;
rotRoot->parent = newRoot;
rotRoot->balanceFactor = rotRoot->balanceFactor + 1 - min(newRoot->balanceFactor, 0);
newRoot->balanceFactor = newRoot->balanceFactor + 1 + max(rotRoot->balanceFactor, 0);
}
void rebalance(TreeNode *node){
if (node->balanceFactor < 0){
if (node->rightChild->balanceFactor > 0){
this->rotateRight(node->rightChild);
this->rotateLeft(node);
}
else{
this->rotateLeft(node);
}
}
else if (node->balanceFactor > 0){
if (node->leftChild->balanceFactor < 0){
this->rotateLeft(node->leftChild);
this->rotateRight(node);
}
else {
this->rotateRight(node);
}
}
}
8.18. Summary of Map ADT Implementations
8.19. Summary
8.20. Discussion Questions
8.21. Programming Exercises
8.22. Glossary
8.23. Matching
9. Graphs and Graph Algorithms
9.1. Objectives
9.2. Vocabulary and Definitions
- Vertex It can have a name, which we will call the “key.” A vertex may also have additional information. We will call this additional information the “payload.”
- Edge An edge connects two vertices to show that there is a relationship between them. Edges may be one-way or two-way. If the edges in a graph are all one-way, we say that the graph is a directed graph, or a digraph.
- Weight A cost to go from one vertex to another.
- Path A path in a graph is a sequence of vertices that are connected by edges.
- Cycle A cycle in a directed graph is a path that starts and ends at the same vertex.
G = (V,E)
V is a set of vertices and E is a set of edges.Each edge is a tuple (v,w) where w,v∈V.
9.3. The Graph Abstract Data Type
A problem that has many applications is finding the shortest paths from each vertex to all other vertices.The Shortest Paths problem is an optimization problem.
An obvious algorithm for this problem would be to determine, for each vertex, the lengths of all the paths
from that vertex to each other vertex, and to compute the minimum of these lengths.
For example, suppose there is an edge from every vertex to every other vertex, to calculate all the paths from one vertex A to another vertex B:
- A has any of (n − 2) vertices to be selected for the next vertex
- the next vertex has any of (n − 3) vertices to be selected
- ...
(n-2)(n-3) ... 1 = (n-2)!
The graph abstract data type (ADT) is defined as follows:
- Graph() creates a new, empty graph.
- addVertex(vert) adds an instance of Vertex to the graph.
- addEdge(fromVert, toVert) Adds a new, directed edge to the graph that connects two vertices.
- addEdge(fromVert, toVert, weight) Adds a new, weighted, directed edge to the graph that connects two vertices.
- getVertex(vertKey) finds the vertex in the graph named vertKey.
- getVertices() returns the list of all vertices in the graph.
- in returns True for a statement of the form vertex in graph, if the given vertex is in the graph, False otherwise.
There are two well-known implementations of a graph,
- the adjacency matrix
- the adjacency list
9.4. An Adjacency Matrix
One of the easiest ways to implement a graph is to use a two-dimensional matrix.We represent a weighted graph containing n vertices by an array W where:
weight on the edge if there is an edge from the vertex i to j
W[i][j] = infinite if there is no edge from the vertex i to j
0 if i= j
The value that is stored in the cell at the intersection of row i and column j indicates if there is an edge from vertex i to vertex j.A value in a cell represents the weight of the edge from vertex i to vertex j.
The adjacency matrix is a good implementation for a graph when the number of edges is large.
If most of the cells in the matrix are empty, this matrix is “sparse”.
A matrix is not a very efficient way to store sparse data.
9.5. An Adjacency List
A more space-efficient way to implement a sparsely connected graph is to use an adjacency list.In an adjacency list implementation,
- A list of all the vertex object in the Graph object is maintained. The std::map is used to record the Vertex object list.
- Each Vertex object mainains a list of the other vertices that it is connected to, and the weight of each edge . The std::map is used to keep track of the weight of each edge.
9.6. Implementation
#include <iostream>
#include <map>
#include <vector>
using namespace std;
class Vertex {
public:
int id;
map<int, int> connectedTo; // (dst, weight)
//Empty constructor.
Vertex() {
}
//Constructor that defines the key of the vertex.
Vertex(int key) {
id = key;
}
//Adds a neighbor to this vertex with the specified ID and weight.
void addNeighbor(int nbr, int weight = 0) {
connectedTo[nbr] = weight;
}
//Returns a vector (e.g, list) of vertices connected to this one.
vector<int> getConnections() {
vector<int> neighbors;
// Use of iterator to find all keys
for (map<int, int>::iterator it = connectedTo.begin();
it != connectedTo.end();
++it) {
neighbors.push_back(it->first);
}
return neighbors;
}
//Returns the ID of this vertex.
int getId() {
return id;
}
//Returns the weight of the connection between this vertex and the specified neighbor.
int getWeight(int nbr) {
return connectedTo[nbr];
}
//Output stream overload operator for printing to the screen.
friend ostream &operator<<(ostream &, Vertex &);
};
ostream &operator<<(ostream &os, Vertex &vert) {
vector<int> connects = vert.getConnections();
os << "( " << vert.id << " : ";
for (unsigned int i = 0; i < connects.size(); i++) {
os << connects[i] << " ";
}
os << ") \n";
return os;
}
class Graph {
public:
map<int, Vertex> vertList;
int numVertices;
//Empty constructor.
Graph() {
numVertices = 0;
}
//Adds the specified vertex and returns a copy of it.
Vertex addVertex(int key) {
numVertices++;
Vertex newVertex = Vertex(key);
this->vertList[key] = newVertex;
return newVertex;
}
//Returns the vertex with the specified ID.
//Will return NULl if the vertex doesn't exist.
Vertex *getVertex(int n) {
std::map<int, Vertex>::iterator it;
it = vertList.find(n);
if ( it != vertList.end()){
// Forced to use pntr due to possibility of returning NULL
Vertex *vpntr = &vertList[n];
return vpntr;
}
return NULL;
}
//Returns a boolean indicating if an index with the specified ID exists.
bool contains(int n) {
std::map<int, Vertex>::iterator it;
it = vertList.find(n);
if ( it != vertList.end())
return true;
return false;
}
//Adds an edge between vertices F and T with a weight equivalent to cost.
void addEdge(int f, int t, int cost = 0) {
if (!this->contains(f)) {
cout << f << " was not found, adding!" << endl;
this->addVertex(f);
}
if (!this->contains(t)) {
cout << t << " was not found, adding!" << endl;
}
vertList[f].addNeighbor(t, cost);
}
//Returns a vector (e.g, list) of all vertices in this graph.
vector<int> getVertices() {
vector<int> verts;
for (map<int, Vertex>::iterator it = vertList.begin();
it != vertList.end();
++it) {
verts.push_back(it->first);
}
return verts;
}
//Overloaded Output stream operator for printing to the screen
friend ostream &operator<<(ostream &, Graph &);
};
ostream &operator<<(ostream &stream, Graph &grph) {
for (unsigned int i = 0; i < grph.vertList.size(); i++) {
stream << grph.vertList[i];
}
return stream;
}
int main() {
Graph g;
for (int i = 0; i < 6; i++) {
g.addVertex(i);
}
g.addEdge(0, 1, 5);
g.addEdge(0, 5, 2);
g.addEdge(1, 2, 4);
g.addEdge(2, 3, 9);
g.addEdge(3, 4, 7);
g.addEdge(3, 5, 3);
g.addEdge(4, 0, 1);
g.addEdge(5, 4, 8);
g.addEdge(5, 2, 1);
cout << g << endl;
return 0;
}
$ ./test
( 0 : 1 5 )
( 1 : 2 )
( 2 : 3 )
( 3 : 4 5 )
( 4 : 0 )
( 5 : 2 4 )
9.7. The Word Ladder Problem
A word ladder puzzle is a game that you transform or morph one word into another word progressively:- Each step consists of a single letter substitution.
- You are not allowed to transform a word into a non-word
FOOL POOL POLL POLE PALE SALE SAGE
9.8. Building the Word Ladder Graph
There is an edge from one word to another word if the two words are only different by a single letter.Assume that we have a list of words that are all the same length:
- Create a vertex in the graph for every word in the list.
- If the two words in question are different by only one letter, we can create an edge between them in the graph. Roughly speaking, comparing one word to every other word on the list is an O(n2) algorithm.
We can do much better by using buckets, only words matching the buccket's label are put in the labeled bucket.
#include <fstream>
#include <iostream>
#include <map>
#include <string>
#include <vector>
using namespace std;
class Vertex {
public:
string id;
map<string, float> connectedTo;
Vertex() {
}
Vertex(string key) {
id = key;
}
void addNeighbor(string nbr, float weight = 1) {
connectedTo[nbr] = weight;
}
vector<string> getConnections() {
vector<string> keys;
// Use of iterator to find all keys
for (map<string, float>::iterator it = connectedTo.begin();
it != connectedTo.end();
++it) {
keys.push_back(it->first);
}
return keys;
}
string getId() {
return id;
}
float getWeight(string nbr) {
return connectedTo[nbr];
}
friend ostream &operator<<(ostream &, Vertex &);
};
ostream &operator<<(ostream &stream, Vertex &vert) {
vector<string> connects = vert.getConnections();
stream << vert.id << " -> ";
for (unsigned int i = 0; i < connects.size(); i++) {
//stream << connects[i] << endl << "\t";
stream << connects[i] << "\t";
}
return stream;
}
class Graph {
public:
map<string, Vertex> vertList;
int numVertices;
bool directional;
Graph(bool directed = true) {
directional = directed;
numVertices = 0;
}
Vertex addVertex(string key) {
numVertices++;
Vertex newVertex = Vertex(key);
this->vertList[key] = newVertex;
return newVertex;
}
Vertex *getVertex(string n) {
for (map<string, Vertex>::iterator it = vertList.begin();
it != vertList.end();
++it) {
if (it->first == n) {
// Forced to use pntr due to possibility of returning NULL
Vertex *vpntr = &vertList[n];
return vpntr;
} else {
return NULL;
}
}
}
bool contains(string n) {
for (map<string, Vertex>::iterator it = vertList.begin();
it != vertList.end();
++it) {
if (it->first == n) {
return true;
}
}
return false;
}
void addEdge(string f, string t, float cost = 1) {
if (!this->contains(f)) {
this->addVertex(f);
}
if (!this->contains(t)) {
this->addVertex(t);
}
vertList[f].addNeighbor(t, cost);
if (!directional) {
vertList[t].addNeighbor(f, cost);
}
}
vector<string> getVertices() {
vector<string> verts;
for (map<string, Vertex>::iterator it = vertList.begin();
it != vertList.end();
++it) {
verts.push_back(it->first);
}
return verts;
}
friend ostream &operator<<(ostream &, Graph &);
};
ostream &operator<<(ostream &stream, Graph &grph) {
cout << "= Display the graph =\n";
for (map<string, Vertex>::iterator it = grph.vertList.begin();
it != grph.vertList.end();
++it) {
stream << it->second;
cout<<endl;
}
return stream;
}
string getBlank(string str, int index) {
string blank = str;
blank[index] = '_';
return blank;
}
Graph buildGraph(vector<string> words) {
Graph g(false);
map<string, vector<string> > bucket_map_vec;
// Go through the words to create buckets
cout << "= Create buckets =\n";
for (unsigned int i = 0; i < words.size(); i++) {
// Go through each letter, making it blank
cout << words[i] << ": ";
for (unsigned int j = 0; j < words[i].length(); j++) {
string bucket = getBlank(words[i], j);
cout << "\t" << bucket;
// Add the word to the map at the location of the blank
bucket_map_vec[bucket].push_back(words[i]);
}
cout << endl;
}
// go through each bucket to add edges in the same bucket
cout << "= Create edges =\n";
for (map<string, vector<string> >::iterator iter = bucket_map_vec.begin(); iter != bucket_map_vec.end(); ++iter) {
if ( iter->second.size() < 2 ) // the edge between 2 vertexes
continue;
cout << iter->first << ": " ;
for(unsigned int i=0; i<iter->second.size();i++) {
for (unsigned int j=0; j<iter->second.size();j++) {
if (iter->second[i]!=iter->second[j]) {
cout << iter->second[i] << "-" << iter->second[j] << "\t";
g.addEdge(iter->second[i],iter->second[j]);
}
}
}
cout << endl;
}
return g;
}
int main() {
// Vector Initialized with an array
string arr[] = {"fool","cool","pool","poll","pole","pall","fall","fail","foil","foul","pope","pale","sale","sage","page"};
vector<string> words(arr,arr+(sizeof(arr)/sizeof(arr[0])));
Graph g = buildGraph(words);
cout << g << endl;
return 0;
}
$ ./test
= Create buckets =
fool: _ool f_ol fo_l foo_
cool: _ool c_ol co_l coo_
pool: _ool p_ol po_l poo_
poll: _oll p_ll po_l pol_
pole: _ole p_le po_e pol_
pall: _all p_ll pa_l pal_
fall: _all f_ll fa_l fal_
fail: _ail f_il fa_l fai_
foil: _oil f_il fo_l foi_
foul: _oul f_ul fo_l fou_
pope: _ope p_pe po_e pop_
pale: _ale p_le pa_e pal_
sale: _ale s_le sa_e sal_
sage: _age s_ge sa_e sag_
page: _age p_ge pa_e pag_
= Create edges =
_age: sage-page page-sage
_ale: pale-sale sale-pale
_all: pall-fall fall-pall
_ool: fool-cool fool-pool cool-fool cool-pool pool-fool pool-cool
f_il: fail-foil foil-fail
fa_l: fall-fail fail-fall
fo_l: fool-foil fool-foul foil-fool foil-foul foul-fool foul-foil
p_le: pole-pale pale-pole
p_ll: poll-pall pall-poll
pa_e: pale-page page-pale
pal_: pall-pale pale-pall
po_e: pole-pope pope-pole
po_l: pool-poll poll-pool
pol_: poll-pole pole-poll
sa_e: sale-sage sage-sale
= Display the graph =
cool -> fool pool
fail -> fall foil
fall -> fail pall
foil -> fail fool foul
fool -> cool foil foul pool
foul -> foil fool
page -> pale sage
pale -> page pall pole sale
pall -> fall pale poll
pole -> pale poll pope
poll -> pall pole pool
pool -> cool fool poll
pope -> pole
sage -> page sale
sale -> pale sage
The list of four-letter words we have for this problem is 15 words long,
- If we were to use an adjacency matrix the matrix would have 15 * 15 = 225 cells.
- The graph constructed by the buildGraph function has exactly 38 edges
9.9. Implementing Breadth First Search
With the graph constructed, we will use it to find the shortest solution to the word ladder problem.
Breadth first search (BFS) is one of the easiest algorithms for searching a graph.
Given a graph G and a starting vertex s, find all the vertices in G for which there is a path from s.
- Find all the vertices that are a distance k from s before it finds any vertices that are a distance k+1. Imagine that it is building a tree: adds all children of the starting vertex before it begins to discover any of the grandchildren.
- To keep track of its progress, BFS colors each of the vertices white, gray, or black.
- All the vertices are initialized to white when they are constructed. A white vertex is an undiscovered vertex.
- When a vertex is initially discovered, it is colored gray A gray node may have some white vertices adjacent to it, indicating that there are still additional vertices to explore.
- When BFS has completely explored a vertex, it is colored black. A black vertex has no white vertices adjacent to it.
How the breadth first tree corresponding to the Word Ladder graph is constructed:
- Starting from "fool" we take all nodes that are adjacent to "fool" and add them to the tree.
{pool, foil, foul, cool}
Each of these nodes are in the same distance from the source, all these nodes are added to a queue whih will be discovered 1-by-1.
- Remove the node "pool" from the queue and discover its neighbors one neighbor "poll" is found and add to the queue.
- Remove the node "foil" from the queue and discover its neighbors one neighbor "fail" is found and add to the queue.
- Remove the node "foul" from the queue and discover its neighbors no node needs to be discovered
- Remove the node "cool" from the queue and discover its neighbors no node needs to be discovered
Graph bfs(Graph g, Vertex *start) {
start->dist = 0;
start->pred = NULL;
queue<Vertex *> vertQueue;
vertQueue.push(start);
while (vertQueue.size() > 0) {
Vertex *currentVert = vertQueue.front();
vertQueue.pop();
for (unsigned int nbr = 0; nbr < currentVert->getConnections().size(); nbr++) {
if (g.vertList[currentVert->getConnections()[nbr]].color == 'w') {
g.vertList[currentVert->getConnections()[nbr]].color = 'g';
g.vertList[currentVert->getConnections()[nbr]].dist =
currentVert->dist + 1;
g.vertList[currentVert->getConnections()[nbr]].pred =
currentVert;
vertQueue.push(&g.vertList[currentVert->getConnections()[nbr]]);
}
}
currentVert->color = 'b';
}
return g;
}
void traverse(Vertex *y) {
Vertex *x = y;
while (x->pred) {
cout << x->id << endl;
x = x->pred;
}
cout << x->id << endl;
}
int main() {
// Vector Initialized with an array
string arr[] = {"fool",
"cool",
"pool",
"poll",
"pole",
"pall",
"fall",
"fail",
"foil",
"foul",
"pope",
"pale",
"sale",
"sage",
"page"};
vector<string> words(arr, arr + (sizeof(arr) / sizeof(arr[0])));
Graph g(false);
g = buildGraph(words);
g = bfs(g, g.getVertex("fool"));
traverse(g.getVertex("pall"));
return 0;
}
9.10. Breadth First Search Analysis
9.11. The Knight’s Tour Problem
在西洋棋上,騎士要如何走過棋盤上每個點,且每個點只能走一次.如果最後能走回原點,則稱為封閉式巡邏(tour is closed),否則稱為開放式巡邏(tour is open).
騎士的走法為:「直走或橫走2格,轉90度再走一格」。走"日字",和象棋中的馬一樣。
所以一個點通常有8種走法 .
- Represent the legal moves of a knight on a chessboard as a graph
- Use a graph algorithm to find a path of length rows × columns−1 where every vertex on the graph is visited exactly once.
9.12. Building the Knight’s Tour Graph
- Each square on the chessboard can be represented as a node in the graph.
- Each legal move by the knight can be represented as an edge in the graph.
9.13. Implementing Knight’s Tour
9.14. Knight’s Tour Analysis
9.15. General Depth First Search
Its goal is to search as deeply as possible, connecting as many nodes in the graph as possible and branching where necessary.
It is even possible that a depth first search will create more than one tree.
The depth first search will make use of two additional instance variables in the Vertex class:
- The discovery time tracks the number of steps in the algorithm before a vertex is first encountered.
- The finish time is the number of steps in the algorithm before a vertex is colored black
9.16. Depth First Search Analysis
9.17. Topological Sorting
9.18. Strongly Connected Components
Greedy Algorithms
A greedy algorithm is a simple, intuitive algorithm that is used in optimization problems.The algorithm makes the local optimal choice at each step as it attempts to find the overall optimal way to solve the entire problem.
Greedy algorithms are quite successful in some problems, such as Huffman encoding which is used to compress data, or Dijkstra's algorithm, which is used to find the shortest path through a graph.
However, in many problems, a greedy strategy does not produce an optimal solution.
For example, in the animation below, the greedy algorithm seeks to find the path with the largest sum.
The greedy algorithm fails to find the largest sum, however, because it makes decisions based only on the information it has at any one step, without regard to the overall problem.
A greedy algorithm can be used to solve the problem if it is true that, at every step, there is a choice that is optimal for the problem up to that step, and after the last step, the algorithm produces the optimal solution of the complete problem.
To make a greedy algorithm,
- Identify an optimal substructure or subproblem in the problem. Then, determine what the solution will include (for example, the largest sum, the shortest path, etc.).
- Create some sort of iterative way to go through all of the subproblems and build a solution.
9.19. Shortest Path Problems
A small example of a weighted graph that represents the interconnection of routers in the Internet.The problem that we want to solve is to find the path with the smallest total weight(time delay) along which to route any given message.
9.20. Dijkstra’s Algorithm
Dijkstra's algorithm is used to find the shortest path between nodes in a graph.This problem has satisfactory optimization substructure:
- A is connected to B, B is connected to C, and the path must go through A and B to get to the destination C
- the shortest path from A to B and the shortest path from B to C must be a part of the shortest path from A to C.
- From the starting node#1
- Calculates the distance through it to each unvisited neighbor, and updates the neighbor's distance if smaller.
- node#2 distance = 7
- node#3 distance = 9
- node#6 distance = 14
- Mark visited (set to red) when done with neighbors
- from the node#2
- Calculates the distance through it to each unvisited neighbor, and updates the neighbor's distance if smaller.
- node#3 distance = 9 (not updated)
- node#4 distance = 22
- Mark visited (set to red) when done with neighbors
- from the node#3
- Calculates the distance through it to each unvisited neighbor, and updates the neighbor's distance if smaller.
- node#4 distance = 20 (updated)
- node#6 distance = 11 (updated)
- Mark visited (set to red) when done with neighbors
- from the node#6
- Calculates the distance through it to each unvisited neighbor, and updates the neighbor's distance if smaller.
- node#5 distance = 20 (updated)
- Mark visited (set to red) when done with neighbors
9.21. Analysis of Dijkstra’s Algorithm
9.22. Prim’s Spanning Tree Algorithm
9.23. Summary
9.24. Discussion Questions
9.25. Programming Exercises
9.26. Glossary
9.27. Matching
C++ Reference
- C library:
- <cassert> (assert.h)
- <cctype> (ctype.h)
- <cerrno> (errno.h)
- <cfenv> (fenv.h)
- <cfloat> (float.h)
- <cinttypes> (inttypes.h)
- <ciso646> (iso646.h)
- <climits> (limits.h)
- <clocale> (locale.h)
- <cmath> (math.h)
- <csetjmp> (setjmp.h)
- <csignal> (signal.h)
- <cstdarg> (stdarg.h)
- <cstdbool> (stdbool.h)
- <cstddef> (stddef.h)
- <cstdint> (stdint.h)
- <cstdio> (stdio.h)
- <cstdlib> (stdlib.h)
- <cstring> (string.h)
- <ctgmath> (tgmath.h)
- <ctime> (time.h)
- <cuchar> (uchar.h)
- <cwchar> (wchar.h)
- <cwctype> (wctype.h)
- Containers(Standard Template Library): The Standard Template Library (STL) is a set of C++ template classes to provide common programming data structures and functions.
- <array>
- <deque>
- <forward_list>
- <list>
- <map>
- <queue>
- <set>
- <stack>
- <unordered_map>
- <unordered_set>
- <vector>
- Input/Output:
- <fstream>
- <iomanip>
- <ios>
- <iosfwd>
- <iostream>
- <istream>
- <ostream>
- <sstream>
- <streambuf>
- Multi-threading:
- <atomic>
- <condition_variable>
- <future>
- <mutex>
- <thread>
- Other:
- <algorithm>
- <bitset>
- <chrono>
- <codecvt>
- <complex>
- <exception>
- <functional>
- <initializer_list>
- <iterator>
- <limits>
- <locale>
- <memory>
- <new>
- <numeric>
- <random>
- <ratio>
- <regex>
- <stdexcept>
- <string>
- std::to_string(val) A string object containing the representation of val as a sequence of characters.
- <system_error>
- <tuple>
- <typeindex>
- <typeinfo>
- <type_traits>
- <utility>
- std::pair (class T1, class T2) The pair container is a simple container consisting of two data elements or objects.
- pair<V1,V2> make_pair (T1&& x, T2&& y); Constructs a pair object with its first element set to x and its second element set to y.
The individual values can be accessed through its public members first and second.
#include <utility> // std::pair
#include <iostream> // std::cout
int main () {
std::pair <int,int> foo;
std::pair <int,int> bar;
foo = std::make_pair (10,20);
bar = std::make_pair (10.5,'A'); // ok: implicit conversion from pair<double,char>
std::cout << "foo: " << foo.first << ", " << foo.second << '\n';
std::cout << "bar: " << bar.first << ", " << bar.second << '\n';
return 0;
}
Defined in header <memory>
- std::unique_ptr Only exactly one copy of an object exists.
- std::shared_ptr A reference counting smart pointer that can be used to store and pass a reference beyond the scope of a function.
C Library
The elements of the C language library are also included as a subset of the C++ Standard library.
- Each header file has the same name as the C language version but with a "c" prefix and no extension. For example, the C++ equivalent for the C language header file <stdlib.h> is <cstdlib>.
- Every element of the library is defined within the std namespace.
strtok
char * strtok ( char * str, const char * delimiters );Split string into tokens.
A sequence of calls to this function split str into tokens, which are sequences of contiguous characters separated by any of the characters that are part of delimiters.
- On a first call, the function expects a C string as argument for str, whose first character is used as the starting location to scan for tokens.
- In subsequent calls, the function expects a null pointer and uses the position right after the end of the last token as the new starting location for scanning.
- Once the terminating null character of str is found in a call to strtok, all subsequent calls to this function (with a null pointer as the first argument) return a null pointer.
/* strtok example */
#include <stdio.h>
#include <string.h>
int main ()
{
char str[] ="- This, a sample string.";
char * pch;
printf ("Splitting string \"%s\" into tokens:\n",str);
pch = strtok (str," ,.-");
while (pch != NULL)
{
printf ("%s\n",pch);
pch = strtok (NULL, " ,.-");
}
return 0;
}
Output:
Splitting string "- This, a sample string." into tokens: This a sample string
Containers
A container is a holder object that stores a collection of other objects (its elements).They are implemented as class templates, templatizing make it generic in the sense that it can store objects of any data type.
The container manages the storage space for its elements and provides member functions to access them, either directly or through iterators.
According to the style of functioning, these container classes can be categorized into :
- Sequence containers A Sequential container, which represents a linear data structure
- array
- vector
- deque
- forward_list
- list
- Container adaptors Adapter container classes provide functions like push and pop that insert and retrieve an element into the storage, respectively.
- stack
- queue
- priority_queue
- Associative containers Associative containers represent a nonlinear data structure with the capability to quickly locate elements stored in the container.
- set
- multiset
- map
- multimap
- Unordered associative containers
- unordered_set
- unordered_multiset
- unordered_map
- unordered_multimap
- Other
- bitset
- valarray
It does not support iterators. Elements are stored simply for storage and retrieval.
These containers can store values as key-value pairs. The keys are immutable and forms the basis for quick search of container elements.
Standard Containers
stack, queue and priority_queue are implemented as container adaptors.Container adaptors are not full container classes, but classes that provide a specific interface relying on an object of one of the container classes (such as deque or list) to handle the elements.
Container class templates
Sequence containers
- array Array class (class template ).
Arrays are fixed-size sequence containers: they hold a specific number of elements ordered in a strict linear sequence.
Therefore, they cannot be expanded or contracted dynamically like vector.
Arrays are initialized in the same way as built-in arrays,
// constructing arrays
#include <iostream>
#include <array>
// default initialization (non-local = static storage):
std::array<int,3> global; // zero-initialized: {0,0,0}
int main ()
{
// default initialization (local = automatic storage):
std::array<int,3> first; // uninitialized: {?,?,?}
// initializer-list initializations:
std::array<int,3> second = {10,20}; // initialized as: {10,20,0}
std::array<int,3> third = {1,2,3}; // initialized as: {1,2,3}
// copy initialization:
std::array<int,3> fourth = third; // copy: {1,2,3}
std::cout << "The contents of fourth are:";
for (auto x:fourth) std::cout << ' ' << x;
std::cout << '\n';
return 0;
}
The contents of fourth are: 1 2 3
// constructing vectors
#include <iostream>
#include <vector>
int main ()
{
// constructors used in the same order as described above:
std::vector<int> first; // empty vector of ints
std::vector<int> second (4,100); // Specifying size and initializing all values
std::vector<int> third (second.begin(),second.end()); // iterating through second
std::vector<int> fourth (third); // a copy of third
std::vector<int> vect{ 10, 20, 30 }; // initialize a vector like an array.
// the iterator constructor can also be used to construct from arrays:
int myints[] = {16,2,77,29};
std::vector<int> fifth (myints, myints + sizeof(myints) / sizeof(int) );
std::cout << "The contents of fifth are:";
for (std::vector<int>::iterator it = fifth.begin(); it != fifth.end(); ++it)
std::cout << ' ' << *it;
std::cout << '\n';
return 0;
}
$ ./test
The contents of fifth are: 16 2 77 29
Container adaptors
- stack LIFO stack (class template )
// constructing stacks
#include <iostream> // std::cout
#include <stack> // std::stack
#include <vector> // std::vector
#include <deque> // std::deque
int main ()
{
std::deque<int> mydeque (3,100); // deque with 3 elements
std::vector<int> myvector (2,200); // vector with 2 elements
std::stack<int> first; // empty stack
std::stack<int> second (mydeque); // stack initialized to copy of deque
std::stack<int,std::vector<int> > third; // empty stack using vector
std::stack<int,std::vector<int> > fourth (myvector);
std::cout << "size of first: " << first.size() << '\n';
std::cout << "size of second: " << second.size() << '\n';
std::cout << "size of third: " << third.size() << '\n';
std::cout << "size of fourth: " << fourth.size() << '\n';
return 0;
}
size of first: 0
size of second: 3
size of third: 0
size of fourth: 2
Associative containers
- std::set Sets are containers that store unique elements following a specific order.
- begin() Returns an iterator to the first element in the set.
- end() Returns an iterator to the theoretical element that follows the last element in the set.
- size() Returns the number of elements in the set.
- max_size() Returns the maximum number of elements that the set can hold.
- empty() Returns whether the set is empty.
- insert(const g) Adds a new element ‘g’ to the set.
- erase(iterator position) Removes the element at the position pointed by the iterator.
- clear() Removes all the elements from the set.
- find(val) Searches the container for an element equivalent to val and returns an iterator to it if found, otherwise it returns an iterator to end().
The value of the elements in a set cannot be modified once in the container (the elements are always const), but they can be inserted or removed from the container.
set containers are generally slower than unordered_set containers to access individual elements by their key, but they allow the direct iteration on subsets based on their order.
Sets are typically implemented as binary search trees.
Some Basic Functions Associated with Set:
#include <set>
#include <iostream>
int main( )
{
using namespace std;
set <int> s1;
set <int>::iterator itr;
set <int>::const_iterator s1_cIter;
s1.insert( 1 );
s1.insert( 2 );
s1.insert( 3 );
s1.insert( 4 );
s1.insert( 5 );
itr = s1.begin( );
cout << "The first element of s1 is " << *itr << endl;
itr = s1.begin( );
s1.erase( itr );
// The following 2 lines would err because the iterator is const
// s1_cIter = s1.begin( );
// s1.erase( s1_cIter );
s1_cIter = s1.begin( );
cout << "The first element of s1 is now " << *s1_cIter << endl;
// assigning the elements from s1 to s2
set<int> s2(s1.begin(), s1.end());
// print all elements of the set s2
cout << "\nThe set s2 after assign from s1 is : \n";
for (itr = s2.begin(); itr != s2.end(); itr++) {
cout << *itr << " ";
}
cout << endl;
itr = s2.find(4);
if ( itr != s2.end() )
cout << "s2 has 4\n";
itr = s2.find(6);
if ( itr == s2.end() )
cout << "s2 doesn't have 6\n";
// remove element with value 50 in s2
int num;
num = s2.erase(4);
cout << "\ns2.erase(4) : ";
cout << num << " removed\n";
for (itr = s2.begin(); itr != s2.end(); itr++) {
cout << *itr << " ";
}
cout << endl;
}
$ ./test
The first element of s1 is 1
The first element of s1 is now 2
The set s2 after assign from s1 is :
2 3 4 5
s2 has 4
s2 doesn't have 6
s2.erase(4) : 1 removed
2 3 5
Some basic functions associated with Map:
- begin() Returns an iterator to the first element in the map
- end() Returns an iterator to the theoretical element that follows last element in the map
- size() Returns the number of elements in the map
- max_size() Returns the maximum number of elements that the map can hold
- empty() Returns whether the map is empty
- insert(keyvalue, mapvalue) Adds a new element to the map
- find(k) Searches the container for an element with a key equivalent to k and returns an iterator to it if found, otherwise it returns an iterator to map::end.
- erase(iterator position) Removes the element at the position pointed by the iterator
- erase(const g) Removes the key value ‘g’ from the map
- clear() Removes all the elements from the map
#include <iostream>
#include <iterator>
#include <map>
using namespace std;
int main()
{
// empty map container
map<int, int> mapA;
// insert elements in random order
mapA[1] = 40;
mapA.insert(pair<int, int>(2, 30));
mapA.insert(pair<int, int>(3, 60));
mapA.insert(pair<int, int>(4, 20));
mapA.insert(pair<int, int>(5, 50));
mapA.insert(pair<int, int>(6, 50));
mapA.insert(pair<int, int>(7, 10));
// printing map mapA
map<int, int>::iterator itr;
cout << "\nThe map mapA is : \n";
cout << "\tKEY\tELEMENT\n";
for (itr = mapA.begin(); itr != mapA.end(); itr++) {
cout << '\t' << itr->first
<< '\t' << itr->second << '\n';
}
cout << endl;
// assigning the elements from mapA to mapB
map<int, int> mapB(mapA.begin(), mapA.end());
// print all elements of the map mapB
cout << "\nThe map mapB after"
<< " assign from mapA is : \n";
cout << "\tKEY\tELEMENT\n";
for (itr = mapB.begin(); itr != mapB.end(); ++itr) {
cout << '\t' << itr->first
<< '\t' << itr->second << '\n';
}
cout << endl;
// remove all elements up to
// element with key=3 in mapB
cout << "\nmapB after removal of"
" elements from the begin to the key=3 : \n";
cout << "\tKEY\tELEMENT\n";
mapB.erase(mapB.begin(), mapB.find(3));
for (itr = mapB.begin(); itr != mapB.end(); ++itr) {
cout << '\t' << itr->first
<< '\t' << itr->second << '\n';
}
// remove all elements with key = 4
int num;
num = mapB.erase(4);
cout << "\nmapB.erase(4) : ";
cout << num << " removed \n";
cout << "\tKEY\tELEMENT\n";
for (itr = mapB.begin(); itr != mapB.end(); ++itr) {
cout << '\t' << itr->first
<< '\t' << itr->second << '\n';
}
cout << endl;
// lower bound and upper bound for map mapA key = 5
cout << "mapA.lower_bound(5) : "
<< "\tKEY = ";
cout << mapA.lower_bound(5)->first << '\t';
cout << "\tELEMENT = "
<< mapA.lower_bound(5)->second << endl;
cout << "mapA.upper_bound(5) : "
<< "\tKEY = ";
cout << mapA.upper_bound(5)->first << '\t';
cout << "\tELEMENT = "
<< mapA.upper_bound(5)->second << endl;
return 0;
}
$ ./test
The map mapA is :
KEY ELEMENT
1 40
2 30
3 60
4 20
5 50
6 50
7 10
The map mapB after assign from mapA is :
KEY ELEMENT
1 40
2 30
3 60
4 20
5 50
6 50
7 10
mapB after removal of elements from the begin to the key=3 :
KEY ELEMENT
3 60
4 20
5 50
6 50
7 10
mapB.erase(4) : 1 removed
KEY ELEMENT
3 60
5 50
6 50
7 10
mapA.lower_bound(5) : KEY = 5 ELEMENT = 50
mapA.upper_bound(5) : KEY = 6 ELEMENT = 50
Unordered associative containers
- unordered_set Unordered Set (class template )
- unordered_multiset Unordered Multiset (class template )
- unordered_map Unordered Map (class template )
- unordered_multimap Unordered Multimap (class template )
map vs unordered_map in C++
| map | unordered_map | |
|---|---|---|
| Ordering | increasing order(default) | no ordering |
| Implementation | Self balancing BST | Hash Table |
| search time | log(n) | Average: O(1), Worst Case: O(n) |
| Insertion time | log(n) + Rebalance | Same as search |
| Deletion time | log(n) + Rebalance | Same as search |
Input/Output Stream Library
Atomics and threading library
Miscellaneous libraries
Standard Library - Miscellaneous headers
Standard Template Library: Algorithms
The header
Sorting
sort
void sort (RandomAccessIterator first, RandomAccessIterator last); void sort (RandomAccessIterator first, RandomAccessIterator last, Compare comp);
- Sorts the elements in the range [first,last) into ascending order. The range used is [first,last), which contains all the elements between first and last, including the element pointed by first but not the element pointed by last.
- "comp" is a binary function that accepts two elements in the range as arguments, and returns a value convertible to bool. The value returned indicates whether the element passed as first argument is considered to go before the second in the specific strict weak ordering it defines.
The function shall not modify any of its arguments.
This can either be a function pointer or a function object.
// sort algorithm example
#include <iostream> // std::cout
#include <algorithm> // std::sort
#include <vector> // std::vector
bool myfunction (int i,int j) {
return (i<j);
}
struct myclass {
bool operator() (int i,int j) {
return (i<j);
}
} myobject;
int main () {
int myints[] = {32,71,12,45,26,80,53,33};
std::vector<int> myvector (myints, myints+8); // 32 71 12 45 26 80 53 33
// using default comparison (operator <):
std::sort (myvector.begin(), myvector.begin()+4); //(12 32 45 71)26 80 53 33
// using function as comp
std::sort (myvector.begin()+4, myvector.end(), myfunction); // 12 32 45 71(26 33 53 80)
// using object as comp
std::sort (myvector.begin(), myvector.end(), myobject); //(12 26 32 33 45 53 71 80)
// print out content:
std::cout << "myvector contains:";
for (std::vector<int>::iterator it=myvector.begin(); it!=myvector.end(); ++it)
std::cout << ' ' << *it;
std::cout << '\n';
return 0;
}
To sort a list of struct items:
typedef struct node node_t;
struct node {
int customer;
int order;
int serv_time;
};
#include <algorithm>
bool node_compare(node_t n1, node_t n2){
if ( (n1.serv_time) < (n2.serv_time) )
return true;
else if ( (n1.serv_time) > (n2.serv_time) )
return false;
else {
return ( (n1.order) < (n2.order) );
}
}
vector<int> jimOrders(vector<vector<int>> orders) {
int i=0;
node_t *tmp=NULL;
vector<int> res;
vector<node_t> list;
for (i=0; i< orders.size(); i++){
tmp = (node_t *) malloc(sizeof(node_t));
tmp->customer = i+1;
tmp->order = orders[i][0];
tmp->serv_time = orders[i][0] + orders[i][1];
list.push_back(*tmp);
}
sort(list.begin(), list.end(), node_compare);
for (i=0; i< list.size(); i++){
cout << list[i].customer << "," << list[i].serv_time << endl;
res.push_back(list[i].customer);
}
return res;
}
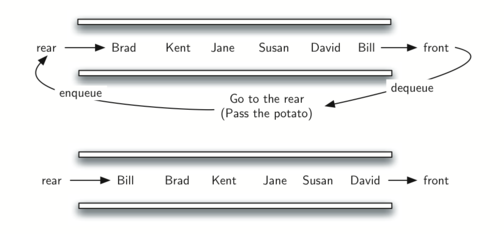





















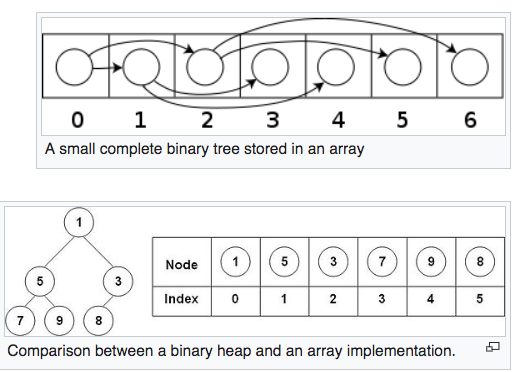





















留言