CRACKING the CODING INTERVIEW: 189 Programming Questions and Solutions
To crack the coding interview, you need to prepare with real interview questions. You must practice on real problems and learn their patterns. It's about developing a fresh algorithm, not memorizing existing problems.
Introduction
The Interview Process
Behind the Scenes
If you're unsure whether or not the phone interview will be technical, ask your recruiting coordinator.
In an on-site interview round, you usually have 3 to 6 in-person interviews. One of these is often over lunch. Your interviewers will provide feedback in some form. Feedback is typically broken down into four categories:
- Analytical Ability
- Coding
- Experience
- Communication
Google puts a strong focus on analytical (algorithm) skills, regardless of experience.
If you have waited more than a week, you should follow up with your recruiter, not responding indicates nothing about your status.
Special Situations
Experienced candidates will be expected to give a more in-depth and an impressive response.
Dev Lead and Managers
Strong coding skills are almost always required for dev lead positions and often for management positions as well.
- Teamwork / Leadership If you come off as too arrogant or too passive, your interviewer may feel you aren't great as a manager.
- Prioritization Prioritization means asking the right questions to understand what is critical and what you can reasonably expect to accomplish.
- Communication You can communicate at many levels and that you can do so in a way that is friendly and engaging.
- Getting Things Done How to structure a project and how to motivate people so you can accomplish the team's goals.
Before the Interview
Preparation Map
- phone interview Locate headset and/or video camera
- Do a final mock interview
- Rephase stories(p. 32)
- Re-read algorithm approaches(p. 67)
- Re-read Big O section(p. 38)
- Continue to practice interview questions
- Review power of 2 (p. 61)
- Remember to talk out loud.
- Write Thank You note to recruiter
- If you haven't heard from recruiter, check in after one week.
Behavioral Questions
Behavioral questions are asked to get to know your personality, to understand your resume more deeply, and just to ease you into an interview.
Interview Preparation Grid
Go through each of the projects or components of your resume and ensure that you can talk about them in detail.| Questions | Project#1 | Project#2 | Project#3 |
| Challenges | |||
| Mistakes/Failures | |||
| Enjoyed | |||
| Leadership | |||
| Conflicts | |||
| What You'd Do Differently |
- The project had challenging components (beyond just "learning a lot").
- You played a central role (ideally on the challenging components).
- You can talk at technical depth.
- What are your weaknesses?
- It may be that I try to find the root cause of a problem. It may cost more time than a workaround. But, it can resolve the real issue to avoid the workaround causing serious problems somedays.
- It may be hard to work with general engineers. I have been a leader and was assigned to work with three other people. While two were great and good, the third team member didn't contribute much. I responded to my manager and the manager discussed to him. But, the situation was still the same. All I can do was to assign non-difficult issues to him and review his code carefully. Besides, he was good in following procedures, I asked him to manage the test environment set-up for certification.
- What questions should you ask the interviewer? "What is the ratio of programming to TAM ? Differences from FAE ?" "What is the interaction with sales and engineers ?" "What opportunities are there at this company to learn about networking applications and deep-learning?"
Responding to Behavioral Questions
- Be Specific, Not Arrogant. Giving just the facts and letting the interviewer derive an interpretation.
- Stay light on details and just state the key points. You can always offer the interviewer the opportunity to drill in further.
- Give Structured Answers Nugget First then the story: S.A.R. (Situation, Action, Result) .
- Tell me about yourself...
Computing Complexity
Time Complexity
The time complexity is the computational complexity that describes the amount of time it takes to run an algorithm.
Big 0, big omega, and big theta describe the upper, lower, and tight bounds for the runtime.
Time complexity is commonly estimated by counting the number of elementary operations performed by the algorithm, supposing that each elementary operation takes a fixed amount of time to perform.
In general, the time complexity is generally expressed as a function of the size of the input, the focus is on the behavior of the complexity when the input size increases : the asymptotic behavior of the complexity.
Therefore, the time complexity is commonly expressed using Big O notation, where n is the input size in units of bits needed to represent the input.
Drop the constants
It is very possible for O(N) code to run faster than O(1) code for specific inputs.Big O just describes the rate of increase.
For ex.,
| MinandMax #1 | MinandMax #2 |
int min = Integer.MAX_VALUE; int max = Integer.MIN_VALUE; for (int x : array) { if (x < min) min = x; if (x > max) max = x; } | int min = Integer.MAX_VALUE; int max = Integer.MIN_VALUE; for (int x : array) { if (x < min) min = x; } for (int x : array) { if (x > max) max = x; } |
#1 is O(N), #2 is O(2N).
But, the first solution #1 has two lines of code per for loop rather than one.
Big O allows us to express how the runtime scales.
Don't consider the instruction's execution time, the constant should be dropped.
Therefore, both solutions are O(N).
Drop the Non-Dominant Terms
The same as "drop the constants", considering the rate of change, you should drop the non-dominant terms.
- O(N2 + N) becomesO(N2)
- O(N + log N) becomesO(N)
Multi-PartAlgorithms: Add vs Multiply
| 0(A + B) | 0(A * B) |
for (int a : arrA) { print(a); } for (int b : arrB) { print(b); } | for (int a: arrA) { for (int b: arrB) { print(a + "," + b); } } |
Amortized Time
An ArrayList, or a dynamically resizing array, will grow as you insert elements.
An Arraylist is implemented with an array. When the array hits capacity, the Arraylist class will create a new array with double the capacity and copy all the elements over to the new array.
You will have to create a new array of size 2N and then copy N elements over.This insertion will take O(N) time.
This worst case happens every once in a while. But once it happens, it won't happen again for so long that the cost is "amortized'.
With N elements in an array, we double the capacity at array sizes 1, 2, 4, 8, 16, ..., N. That doubling takes, respectively, 1, 2, 4, 8, 16, 32, 64, ..., N copies.
1 + 2 + 4 + ... + Nis equivalent to
N + N/2 + N/4 + ... + 1Therefore, N insertions take 0(2N) time. The amortized time for each insertion is 0(1)
Log N Runtimes
We commonly see O(log N) in runtimes. Where does this come from ?
In binary search, we are looking for an example x in an N-element sorted array.
- We first compare x to the midpoint of the array.
- If x == middle, then we return.
- If x < middle, then we search on the left side of the array.
- If x > middle, then we search on the right side of the array.
N
N/2
N/(2*2)
...
4
2
1
When you see a problem where the number of elements in the problem space gets halved each time, that will likely be a O(log N) runtime.2 exp(k) = N K = log2(N)
Recursive Runtimes
Consider the example,
int f(int n) {
if (n <= 1) {
return 1;
}
return f(n - 1) + f(n - 1);
}
This function will expand as a binary tree.
T(N) = O(1) + 2 * T(N-1)
= O(1) + 2*2 * T(N-2)
= ...
= O(1) + 2 exp(N) * T(0)
Therefore, this gives us O( 2 exp(N) ).When you have a recursive function that makes multiple calls to itself, the runtime will often (but not always) look like O( branches * exp(depth) ).
Examples and Exercises
- Sorting each string is O(s * (log s)).
- There are a strings to be sorted, it gives O( a * (s * (log s)) ).
- After the array's element is sorted, Each string comparison takes O(s) time. There are O(a log a)comparisons, therefore this will take O(a*s (log a))time.
- Vl.1
- Vl.2
- Vl.3
- Vl.4
- Vl.
- Vl.
- Vl.
- Vl.
- Vl.
- Vl.
- Vl.
- Vl.
void foo(int[] array) {
int sum = 0;
int product = 1;
for (inti= 0; i < array.length; i++) {
sum =+ array[i);
}
for (int i= 0; i < array.length; i++) {
product*= array[i];
}
System.out.println(sum + ", " + product);
}
This will take O(N) time. (ignore the leading constant 2)
void printPairs(int[] array) {
for (int i= 0; i < array.length; i++) {
for (int j = 0; j < array.length; j++) {
System.out.println(array[i] + "," + array[j]);
}
}
}
O (N*N )
void printUnorderedPairs(int[] array) {
for (int i= 0; i < array.length; i++) {
for (int j= i + 1; j < array.length; j++) {
System.out.println(array[i] + "," + array[j]);
}
}
}
The number of steps total is: (N-1) + (N-2) + (N-3) + ... + 2 + 1 = ( (N-1) + 1 ) * (N-1) / 2 = N(N-1)/2This give O(N*N). By visualizing what it does when N=8,
(0, 1) (0, 2) (0, 3) (0, 4) (0, 5) (0, 6) (0, 7)
(1, 2) (1, 3) (1, 4) (1, 5) (1, 6) (1,'7)
(2, 3) (2, 4) (2, 5) (2, 6) (2, 7)
(3, 4) (3, 5) (3, 6) (3, 7)
(4, 5) (4, 6) (4, 7)
(5, 6) (5, 7)
(6, 7)
This looks like half of an N x N matrix of pairs for iterations. By averaging work, the steps the inner loop does: N-1, N-2, ...2, 1The average steps the inner loop does is (N/2). The outer loop does N steps so that the total steps is N*N/2.
void printUnorderedPairs(int[] arrayA, int][ arrayB) {
for (inti= 0; i < arrayA.length; i++) {
for (int j = 0; j < arrayB.length; j++) {
if (arrayA[i] < arrayB[j]) {
System.out.println(arrayA[i] + "," + arrayB[j]);
}
}
}
}
O( a*b)
void printUnorderedPairs(int[] arrayA, int][ arrayB) {
for (inti= 0; i < arrayA.length; i++) {
for (int j = 0; j < arrayB.length; j++) {
for (int k= 0; k < 100000; k++) {
System.out.println(arrayA[i] + "," + arrayB[j]);
}
}
}
}
O(a*b). (Ignore the leading constant 100000)
void reverse(int[] array) {
for (inti= 0; i <array.length/ 2; i++) {
int other= array.length - i - 1;
int temp= array[i];
array[i] = array[other];
array[other] = temp;
}
}
O(N).
The followings are equivalent to O(N) O(N + P), where P < N/2 O(2N) O(N + log N)Consider an array of strings, every string is to be sorted and the the array is to be sorted. Let s be the length of the longest string and a be the length of the array.
int sum(Node node) { if (node == null) { return 0; } return sum(node.left) + node.value + sum(node.right); }This tells you the number of nodes but the length of input elements. It gives O(N). 試除法﹝埃拉托斯特尼篩法﹞: Check if a number is prime by checking for divisibility on numbers less than it. It only needs to go up to the square root of n because if n is divisible by a number greater than its square root then it's divisible by something smaller than it.
int is_prime(int x){
if(x <= 1) return 0; /* 1不是質數,且不考慮負整數與0,故輸入 x<=1 時輸出為假 */
for(int i = 2; i * i <= x; i++)
if(x % i == 0) return 0; /* 若整除時輸出為假,否則輸出為真 */
return 1;
}
This runs in O( n exp(1/2) ) time.
int factorial(int n) { if (n < 0) { return -1; } else if (n == 0) { return 1; } else { return n * factorial(n - 1); } }It will take O(n) time.
void permutation(String str) { permutation(str, ""); }
int fib(int n) { if (n <= 0) return 0; else if (n == 1) return 1; return fib(n - 1) + fib(n - 2);
n
(n-1) (n-2)
(n-2)(n-3) (n-3)(n-4)
......
1 + 2 exp(1) + 2 exp(2) + ... 2 exp(n-1)
= 2 exp(n)
O( 2 exp(N) )
void allFib(int n) {
for (int i= 0; i < n; i++) {
System.out.println(i + ": "+ fib(i));
}
}
int fib(int n) {
if (n <= 0)
return 0;
else if (n == 1)
return 1;
return fib(n - 1) + fib(n - 2);
}
1 + 2 exp(2) + 2 exp(3) + ... + 2 exp(n)
O( 2 exp(N) )
void allFib(int n) {
int[] memo = new int[n + 1];
for(inti= 0;i< n;i++){
System.out.println(i + ": "+ fib(i, memo));
}
}
int fib(int n, int[] memo) {
if (n =< 0)
return 0;
else if (n== 1)
return 1;
else if (memo[n] > 0)
return memo[n];
memo[n]= fib(n - 1, memo)+ fib(n - 2, memo);
return memo[n];
}
memo is used to memorize the last computed value, only one recursive call is called for each node. 0 + 1 + 2 + 3 + ... This is O(n) time.
The following function prints the powers of 2 from 1 through n (inclusive). For example, if n is 4, it would print 1, 2, and 4. int powers0f2(int n) { if (n < 1) { return 0; } else if (n == 1) { System.out.println(l); return 1; } else { int prev = powers0f2(n / 2); int curr = prev * 2; System.out.println(curr); return curr; } }The runtime is O(log n).
TechnicalQuestions
What You Need To Know
Here's a list of the absolute, must-have knowledge:
- Data Structures
- Linked Lists
- Tree, Tries and Graphs
- Stacks and Queues
- Stack 71. Simplify Path
- Queue 622. Design Circular Queue
- Heaps
- Vectors and ArrayLists
- Hash Tables
- Algorithms
- Breadth-First Search
- Depth-First Search
- Binary Search
- Merge Sort 215. Kth Largest Element in an Array
- Quick Sort
- Concepts
- Bit Manipulation
- Memory (Stack vs. Heap)
- Recursion
- Dynamic Programming
- Big O Time and Space complexity
Powers of 2 Table:
1 million
| Power of 2 | Value | Approximate | bits |
| 10 | 1,024(0x 400) | 1 thousand | 1 Kb |
| 20 | 1,048,576(0x 100000) | 1 Mb | |
| 30 | 1,073,741,824(0x 40000000) | 1 billion | 1 Gb |
| 40 | 1,099,511,627,776(0x 10000000000) | 1 trillion | 1 TB |
The Offer and Beyond
Interview Questions
This covers the following:
- Data Structures Chapter1 ~ Chapter 4
- Concepts and Algorithms Chapter 5 ~ Chapter 11
- Knowledge Based Chapter 12 ~ Chapter 15
- Additional Review Chapter 16 ~ Chapter 17
- 6th Edition: https://github.com/gaylemcd/CtCI-6th-Edition
- 5th Edition: https://github.com/gaylemcd/ctci
Chapter 1 Arrays and Strings
Hash Tables
A hash table is a data structure that maps keys to values for highly efficient lookup. ( ref: 1 and 2 )
The simple implementation(ref) is to use an array of linked lists and a hash code function :
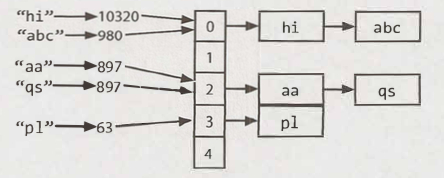
- Compute the key's hash value different keys may have the same hash value
- Map the hash value to an array's index hash(key) % array_length.
- Each element in an array is a linked list to store the key and value for the same hash(key)
The hash table can be implemented by a balanced binary search tree, this gives O( log(N) ). This may save more space than a large fixed array which may not use all elements.
ArrayList and Resizable Arrays
An ArrayList is an array that resizes itself as needed.( dynamically resizable arrays/lists )
The difference between a built-in array and an ArrayList in Java, is that the size of an array cannot be modified (if you want to add or remove elements to/from an array, you have to create a new one). While elements can be added and removed from an ArrayList whenever you want.
The ArrayList class has many useful methods:
- add()
- get(()
- set()
- remove()
- clear()
- size()
Arraylist<String> merge(String[] words, String[] more) {
Arraylist<String> sentence= new Arraylist<String>();
for (String w : words)
sentence.add(w);
for (String w: more)
sentence.add(w);
return sentence;
}
This still providing O(1) time complexity because the total number of copies to insert N elements is roughly:N/2 + N/4 + N/8 + . . . + 2 + 1which is just less than N.
Therefore, inserting N elements takes O(N) work total. Each insertion is O(1) on average.
StringBuilder
Assume that the strings are all the same length (call this l) and that there are n strings.
String joinWords(String[] words) {
String sentence = "";
for (String w: words) {
sentence = sentence + w;
}
return sentence;
}
On each concatenation, a new copy of the string is created, and the two strings are copied over, character by character.l + 2l + 3l + ... + nl = l( 1+ 2 +3 + ... +n) = l( 1 + n ) n/2This reduces to O(l* n*n).
Interview Questions
Chapter 2 Linked Lists
A linked list is a data structure that represents a sequence of nodes.
- A singly linked list each node points to the next node in the linked list.
- A doubly linked list each node points to both the next node and the previous node.
typedef struct node {
int val;
struct node * next;
} node_t;
Init the head node:
node_t *head = NULL;
int init_list( int val ){
head = malloc(sizeof(node_t));
if (head == NULL) {
return 1;
}
head->val = 1;
head->next = NULL;
}
Append a node:
int add_list( int val ){
node_t *node = NULL;
node_t * current = head;
while (current->next != NULL) {
current = current->next;
}
current->next = malloc(sizeof(node_t));
if ( ! current->next )
return 1;
current->next->val = val;
current->next->next = NULL;
return 0;
}
Interview Questions
Chapter 3 Stacks and Queues
A stack uses LIFO (last-in first-out) ordering.
It uses the following operations:
- pop() Remove the top item from the stack.
- push(item) Add an item to the top of the stack.
- peek() Return the top of the stack.
- isEmpty() Return true if and only if the stack is empty.
A queue implements FIFO (first-in first-out) ordering.
It uses the operations:
- add(iterm) Add an item to the end of the list.
- remove() Remove the first item in the list.
- peek( ) Return the top of the queue.
- is Empty() Return true if and only if the queue is empty.
A queue can also be implemented with an array or linked list.
Interview Questions
Chapter 4 Trees and Graphs
Types of Trees
A nice way to understand a tree is with a recursive explanation. A tree is a data structure composed of nodes.- Each tree has a root node.
- The root node has zero or more child nodes.
- Each child node has zero or more child nodes, and so on.
#define CHILDS 2
struct node
{
int data;
struct node children[CHILDS];
};
struct node *head = NULL;
A linked list is a chain of nodes connect through "next" pointers.A tree is similar, but each node can be connected to multiple nodes.
A node of a binary tree is represented by a structure containing a data part and two pointers to other structures of the same type.
struct node
{
int data;
struct node *left;
struct node *right;
};
二元搜尋樹(英語:Binary Search Tree),也稱為有序二元樹(ordered binary tree)或排序二元樹(sorted binary tree),是指一棵空樹或者具有下列性質的二元樹:- 若任意節點的左子樹不空,則左子樹上所有節點的值均小於它的根節點的值;
- 若任意節點的右子樹不空,則右子樹上所有節點的值均大於它的根節點的值;
- 任意節點的左、右子樹也分別為二元搜尋樹;
- 沒有鍵值相等的節點。
(any key stored in the left sub-tree) < (the key in each node) < (any key stored in the right sub-tree)
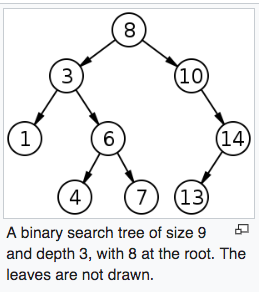
Searching a binary search tree for a specific key can be programmed recursively or iteratively.
- recursively
def search_recursively(key, node): if node is None or node.key == key: return node if key < node.key: return search_recursively(key, node.left) # key > node.key return search_recursively(key, node.right)
def search_iteratively(key, node):
current_node = node
while current_node is not None:
if key == current_node.key:
return current_node
if key < current_node.key:
current_node = current_node.left
else: # key >= current_node.key:
current_node = current_node.right
return current_node
Binary Tree Traversal
- in-order To "visit" (often, print) the left branch, then the current node, and finally, the right branch.
void inOrderTraversal(TreeNode node) { if (node!= null) { inOrderTraversal(node.left); visit(node); inOrderTraversal(node.right); } }
void preOrderTraversal(TreeNode node) { if (node!= null) { visit(node); preOrderTraversal(node.left); preOrderTraversal(node.right); } }
void preOrderTraversal(TreeNode node) { if (node!= null) { preOrderTraversal(node.left); preOrderTraversal(node.right); visit(node); } }Comparisons of the node traversal:
O
/
O
/ \
O O
/\ /\
O O O O
| in-order | pre-order | post-order |
8 4 2 5 1 3 6 7 | 1 2 3 6 4 5 7 8 | 8 7 3 6 1 2 4 5 |
- Start from root.
- Compare the inserting element with root, if less than root, then recurse for left, else recurse for right.
- After reaching end, just insert that node at left(if less than current) else right.
#include<stdio.h>
#include<stdlib.h>
struct node
{
int key;
struct node *left, *right;
};
// A utility function to create a new BST node
struct node *newNode(int item)
{
struct node *temp = (struct node *) malloc(sizeof(struct node));
temp->key = item;
temp->left = temp->right = NULL;
return temp;
}
// A utility function to do inorder traversal of BST
void inorder(struct node *root)
{
if (root != NULL)
{
inorder(root->left);
printf("%d \n", root->key);
inorder(root->right);
}
}
/* A utility function to insert a new node with given key in BST */
struct node* insert(struct node* node, int key)
{
/* If the tree is empty, return a new node */
if (node == NULL)
return newNode(key);
/* Otherwise, recur down the tree */
if (key < node->key) {
node->left = insert(node->left, key);
}else // (key >= node->key) {
node->right = insert(node->right, key);
}
/* return the (unchanged) node pointer */
return node;
}
// Driver Program to test above functions
int main()
{
/* Let us create following BST
50
/ \
30 70
/ \ / \
20 40 60 80 */
struct node *root = NULL;
root = insert(root, 50);
insert(root, 30);
insert(root, 20);
insert(root, 40);
insert(root, 70);
insert(root, 60);
insert(root, 80);
// print inoder traversal of the BST
inorder(root);
return 0;
}
這個例子告訴我們, root的key及插入node的順序會決定tree如何往下延伸.Binary Heaps (Min-Heaps and Max-Heaps)
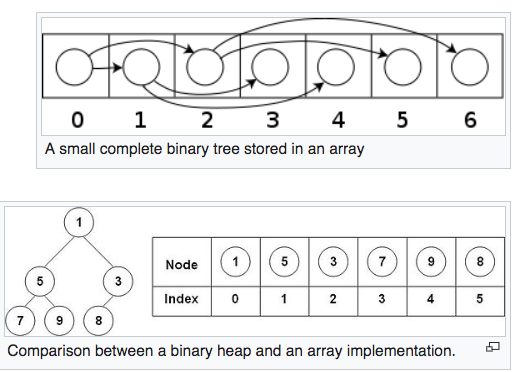
A binary heap is a heap data structure that takes the form of a binary tree. Binary heaps are a common way of implementing priority queues. A binary heap is defined as a binary tree with two additional constraints:- Shape A binary heap is a complete binary tree; that is, all levels of the tree, except possibly the last one (deepest) are fully filled, and, if the last level of the tree is not complete, the nodes of that level are filled from left to right.
- Heap The key stored in each node is either ">=" or "<=" the keys in the node's children.
Note that this inequality must be true for all of a node's descendents, not just its immediate children.
This feature make the top node is always the min/max value in the tree.
Heaps where the parent key is ">=" the child keys are called max-heaps; those where it is "<=" are called min-heaps. 
Heap operations:
- Insert We insert at the rightmost spot so that the complete tree property is maintained. To add an element to a heap we must perform an up-heap operation:
- Add the element to the bottom level of the heap.
- Compare the added element with its parent; if they are in the correct order, stop.
- If not, swap the element with its parent and return to the previous step.
- Extract The procedure for removing the root from the heap and restoring the properties is called down-heap.
- Replace the root of the heap with the last element on the last level: the fartest right node on the lowest level of the Binary Tree.
- Compare the new root with its children; if they are in the correct order, stop.
- If not, swap the element with one of its children and return to the previous step. (Swap with its smaller child in a min-heap and its larger child in a max-heap.)
- Delete a node from the array (this creates a "hole" and the tree is no longer "complete")
- Replace the deletion node with the "fartest right node" on the lowest level of the Binary Tree (This step makes the tree into a "complete binary tree")
- min-Heapify (fix the heap)
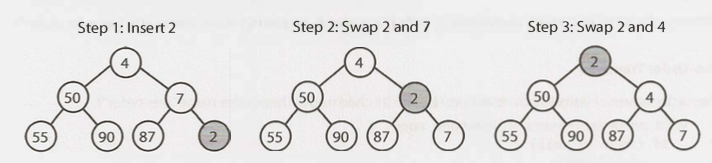
if ( value in replacement node < its parent node )
Move the replacement node UP the binary tree
else
Move the replacement node DOWN the binary tree
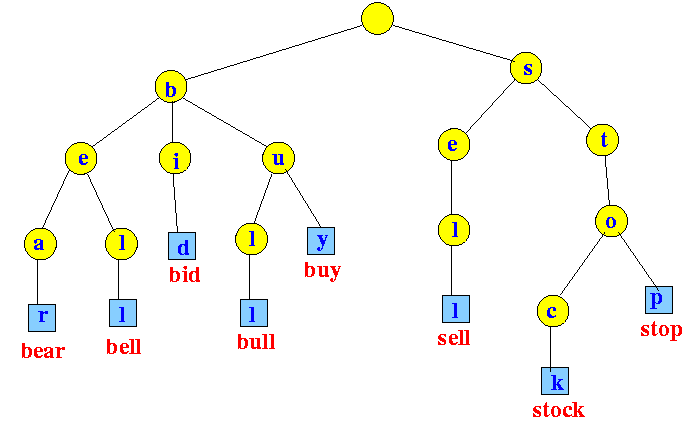
Trie( Prefix Tree )
A trie is a variant of an n-ary tree in which characters are stored at each node. Each path down the tree may represent a word.
It is also known as a prefix tree as all descendants of a node have a common prefix of a string associated with that node, and the root is associated with a empty NULL string.
#include <stdio.h> // define character size // currently Trie supports lowercase English characters (a - z) #define CHAR_SIZE 26 // A Trie node struct Trie { int isLeaf; // 1 when node is a leaf node: end of a string struct (Trie *) character[CHAR_SIZE]; }; // Function that returns a new Trie node struct Trie* getNewTrieNode() { struct Trie* node = (struct Trie*)malloc(sizeof(struct Trie)); node->isLeaf = 0; for (int i = 0; i < CHAR_SIZE; i++) node->character[i] = NULL; return node; } // Iterative function to insert a string in Trie. void insert(struct Trie* *head, char* str) { int index=0; // start from root node struct Trie* trie = *head; while (*str) { index = *str - 'a' // create a new node if path doesn't exists if (trie->character[index] == NULL) trie->character[index] = getNewTrieNode(); // go to next node trie = trie->character[index]; // move to next character str++; } // mark trie node as leaf trie->isLeaf = 1; } // Iterative function to search a string in Trie. It returns 1 // if the string is found in the Trie, else it returns 0 int search(struct Trie* head, char* str) { // return 0 if Trie is empty if (head == NULL) return 0; struct Trie* curr = head; while (*str) { // go to next node curr = curr->character[*str - 'a']; // if string is invalid (reached end of path in Trie) if (curr == NULL) return 0; // move to next character str++; } // str may be a prefix or a sub-string of a word // if current node is a leaf and we have reached the // end of the string, return 1 return curr->isLeaf; } // returns 1 if given node has any children int haveChildren(struct Trie* curr) { for (int i = 0; i < CHAR_SIZE; i++) if (curr->character[i]) return 1; // child found return 0; } // Recursive function to delete a string in Trie. int deletion(struct Trie* *curr, char* str) { // return if Trie is empty if (*curr == NULL) return 0; // if we have not reached the end of the string if (*str) { // recur for the node corresponding to next character in // the string and if it returns 1, delete current node // (if it is non-leaf) if (*curr != NULL && (*curr)->character[*str - 'a'] != NULL && deletion(&((*curr)->character[*str - 'a']), str + 1 ) && (*curr)->isLeaf == 0) { if (!haveChildren(*curr)) { free(*curr); (*curr) = NULL; return 1; } else { return 0; } } } // if we have reached the end of the string if (*str == '\0' && (*curr)->isLeaf) { // if current node is a leaf node and don't have any children if (!haveChildren(*curr)) { free(*curr); // delete current node (*curr) = NULL; return 1; // delete non-leaf parent nodes } // if current node is a leaf node and have children else { // mark current node as non-leaf node (DON'T DELETE IT) (*curr)->isLeaf = 0; return 0; // don't delete its parent nodes } } return 0; } // Trie Implementation in C - Insertion, Searching and Deletion int main() { struct Trie* head = getNewTrieNode(); insert(&head, "hello"); printf("%d ", search(head, "hello")); // print 1 insert(&head, "helloworld"); printf("%d ", search(head, "helloworld")); // print 1 printf("%d ", search(head, "helll")); // print 0 (Not present) insert(&head, "hell"); printf("%d ", search(head, "hell")); // print 1 insert(&head, "h"); printf("%d \n", search(head, "h")); // print 1 + newline deletion(&head, "hello"); printf("%d ", search(head, "hello")); // print 0 (hello deleted) printf("%d ", search(head, "helloworld")); // print 1 printf("%d \n", search(head, "hell")); // print 1 + newline deletion(&head, "h"); printf("%d ", search(head, "h")); // print 0 (h deleted) printf("%d ", search(head, "hell")); // print 1 printf("%d\n", search(head, "helloworld")); // print 1 + newline deletion(&head, "helloworld"); printf("%d ", search(head, "helloworld")); // print 0 printf("%d ", search(head, "hell")); // print 1 deletion(&head, "hell"); printf("%d\n", search(head, "hell")); // print 0 + newline if (head == NULL) printf("Trie empty!!\n"); // Trie is empty now printf("%d ", search(head, "hell")); // print 0 return 0; }
Graphs
A graph is an abstract data type that is meant to implement the undirected graph and directed graph concepts from mathematics; specifically, the field of graph theory.
A graph data structure consists of a finite (and possibly mutable) set of vertices (also called nodes or points), together with a set of ordered/unordered pairs of these vertices.
These pairs are known as edges (also called links or lines), and for a directed graph are also known as arrows.
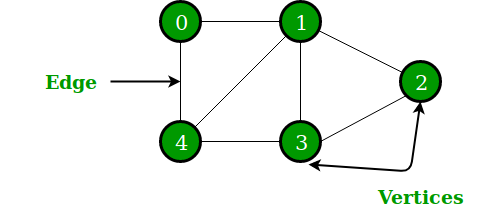
In the above Graph,
- the set of vertices V = {0,1,2,3,4}
- the set of edges E = {01, 12, 23, 34, 04, 14, 13}.
In terms of programming, there are two common ways to represent a graph:
- Adjacency List An adjacency list is an array of separate lists.
Each element of the array A[i] is a list, which contains all the vertices that are adjacent to vertex i.
#include <stdio.h>
#include <stdlib.h>
// A structure to represent an adjacency list node
struct AdjListNode
{
int dest; // adjacent node
struct (AdjListNode *) next;
};
// A structure to represent an adjacency list
struct AdjList
{
struct (AdjListNode *) head;
};
// A structure to represent a graph. A graph
// is an array of adjacency lists.
// Size of array will be V (number of vertices
// in graph)
struct Graph
{
int V;
struct (AdjList *) array;
};
// A utility function to create a new adjacency list node
struct AdjListNode* newAdjListNode(int dest)
{
struct AdjListNode* newNode =
(struct AdjListNode*) malloc(sizeof(struct AdjListNode));
newNode->dest = dest;
newNode->next = NULL;
return newNode;
}
// A utility function that creates a graph of V vertices
struct Graph* createGraph(int V)
{
struct Graph* graph =
(struct Graph*) malloc(sizeof(struct Graph));
graph->V = V;
// Create an array of adjacency lists. Size of
// array will be V
graph->array =
(struct AdjList*) malloc(V * sizeof(struct AdjList));
// Initialize each adjacency list as empty by
// making head as NULL
int i;
for (i = 0; i < V; ++i)
graph->array[i].head = NULL;
return graph;
}
// Adds an edge to an undirected graph
void addEdge(struct Graph* graph, int src, int dest)
{
// Add an edge from src to dest. A new node is
// added to the adjacency list of src. The node
// is added at the begining
struct AdjListNode* newNode = newAdjListNode(dest);
newNode->next = graph->array[src].head;
graph->array[src].head = newNode;
// Since graph is undirected, add an edge from
// dest to src also
newNode = newAdjListNode(src);
newNode->next = graph->array[dest].head;
graph->array[dest].head = newNode;
}
// A utility function to print the adjacency list
// representation of graph
void printGraph(struct Graph* graph)
{
int v;
for (v = 0; v < graph->V; ++v)
{
struct AdjListNode* pCrawl = graph->array[v].head;
printf("\n Adjacency list of vertex %d\n head ", v);
while (pCrawl)
{
printf("-> %d", pCrawl->dest);
pCrawl = pCrawl->next;
}
printf("\n");
}
}
// Driver program to test above functions
int main()
{
// create the graph given in above fugure
int V = 5;
struct Graph* graph = createGraph(V);
addEdge(graph, 0, 1);
addEdge(graph, 0, 4);
addEdge(graph, 1, 2);
addEdge(graph, 1, 3);
addEdge(graph, 1, 4);
addEdge(graph, 2, 3);
addEdge(graph, 3, 4);
// print the adjacency list representation of the above graph
printGraph(graph);
return 0;
}
Graph Search
Typical higher-level operations performed on a graph include finding a path between two nodes via either depth-first or breadth-first search and finding the shortest path between two nodes.
- Breadth-First Search (BFS) BFS is the most commonly used approach. In BFS, node A visits each of A's neighbors before visiting any of their neighbors.
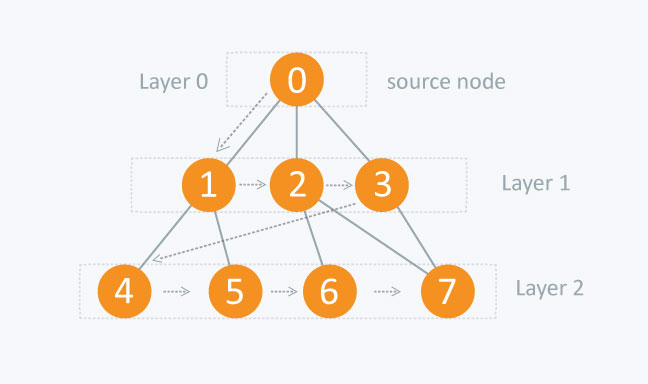
In BFS, you must traverse all the nodes in layer 1 before you move to the nodes in layer 2.
We can use a queue(FIFO) to store the traversing order for a layer such that we can traverse the corresponding child nodes in a similar order.
Given a graph G and a specific source vertex s, the BFS searches through those vertices adjacent to s, then searches the vertices adjacent to those vertices, and so on.
To avoid processing of same node again, use a boolean variable which marks the node after it is visited .
void search(Node source) {
Queue queue = new Queue();
queue.enqueue(source); // Add to the end of queue
print(source)
source.visited= true;
source.distance = 0;
while (!queue.isEmpty()) { // O(V)
Node r= queue.dequeue(); // Remove from the queue
print(r);
// neighbors will be visited now
foreach (Node n in r.adjacent) { // O(E)
if (n.visited == false) {
queue.enqueue(n); // Stores n in queue to further visit its neighbor
print(n)
n.visited= true;
n.distance = r.distance + 1;
}
}
}
}
Because each vertex and edge is visited at most once, the time complexity of a generic BFS algorithm is O(V + E), assuming the graph is represented by an adjacency list. If all the edges in a graph are of the same weight, then BFS can also be used to find the minimum distance between the nodes in a graph.
We visit a node A and then iterate through each of A's neighbors.
When visiting a node B which is a neighbor of A, we visit all of B's neighbors before going on to A's other neighbors.
We must check if the node has been visited. If we don't, we risk getting stuck in an infinite loop.
void search_deeply(Node r) {
if (r == null)
return;
print(r);
r.visited= true;
for each (Node n in r.adjacent) {
if (n.visited == false) {
search_deeply(n);
}
}
}
void visitDFS(Node source){
print(source)
source.visited= true;
source.distance = 0;
for each (Node n in source.adjacent) { // O(V)
if (n.visited == false) {
search_deeply(n); // O(E)
}
}
}
Because each vertex and edge is explored exactly once, the time complexity of a generic DFS algorithm is O(V + E) assuming the use of an adjacency list.
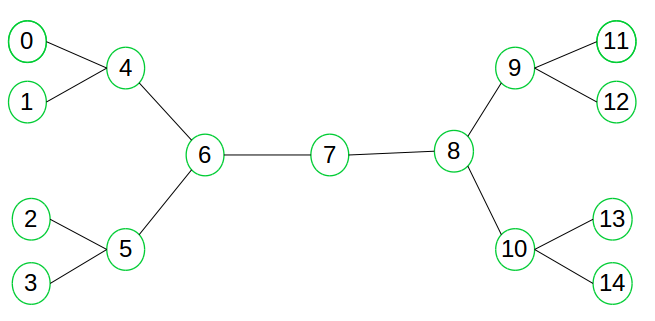 Suppose we want to find if there exists a path from vertex 0 to vertex 14. Here we can execute two searches, one from vertex 0 and other from vertex 14. When both forward and backward search meet at vertex 7, we know that we have found a path from node 0 to 14 and search can be terminated now. Why does it dramatically reduce the amount of required exploration? Suppose if branching factor of tree is b and distance of goal vertex from source is d, for a graph without adjacency list, the normal BFS/DFS searching complexity would be O( b exp(d) ). With bidirectional BFS search, the complexity would be O( 2 * b exp(d/2) ). Below is the pseudocode of the Bidirectional Search:
Suppose we want to find if there exists a path from vertex 0 to vertex 14. Here we can execute two searches, one from vertex 0 and other from vertex 14. When both forward and backward search meet at vertex 7, we know that we have found a path from node 0 to 14 and search can be terminated now. Why does it dramatically reduce the amount of required exploration? Suppose if branching factor of tree is b and distance of goal vertex from source is d, for a graph without adjacency list, the normal BFS/DFS searching complexity would be O( b exp(d) ). With bidirectional BFS search, the complexity would be O( 2 * b exp(d/2) ). Below is the pseudocode of the Bidirectional Search:
void bi_search(Node src1, Node src2) {
Queue queue1 = new Queue();
queue1.enqueue(src1); // Add to the end of queue
print(src1)
src1.visited= true;
src1.distance = 0;
Queue queue2 = new Queue();
queue2.enqueue(src2); // Add to the end of queue
print(src2)
src2.visited= true;
src2.distance = 0;
while ( !queue1.isEmpty() && !queue2.isEmpty() ) { // O(V)
if ( !queue1.isEmpty() ) {
Node r1= queue1.dequeue(); // Remove from the queue
print(r1);
if ( (r1 == src2) || (queue2.has(r1)) ) // intersect
return 0
// neighbors will be visited now
foreach (Node n in r1.adjacent) { // O(E)
if (n.visited == false) {
queue2.enqueue(n); // Stores n in queue to further visit its neighbor
print(n)
n.visited= true;
n.distance = r1.distance + 1;
}
if ( !queue2.isEmpty() ) {
Node r2= queue2.dequeue(); // Remove from the queue
print(r2);
if ( (r2 == src1) || (queue1.has(r2)) ) // intersect
return 0
// neighbors will be visited now
foreach (Node n in r2.adjacent) { // O(E)
if (n.visited == false) {
queue2.enqueue(n); // Stores n in queue to further visit its neighbor
print(n)
n.visited= true;
n.distance = r2.distance + 1;
}
}
}
return 1;
}
Chapter 5 Bit Manipulation
Bit Manipulation By Hand
Tests:
- 0110 + 0010 1000
- 0110 + 0110 1100.
- 0011 + 0010 0101
- 0110 - 0011 0011
- 1101 >> 2 0011
- 1101 ^(~1101) 1111
- 1000 - 0110 0010
- 1101 ^ 0101 1000
- 1011 & (~0 << 2) 1000
- 0011 * 0101 1111
- 0011 * 0011 1001
- 0100 * 0011 1100.
This is equivalent to : (0110 << 1)
This is equivalent to mutiply 4(0100) by 0011.
(0011 << 2)
Bit Facts and Tricks
The followings are all TRUE:X ^ 0s = X X & 0s = 0 X | 0s = X X ^ ls = ~x X & ls = X X | ls = ls X ^ X = 0 X & X = X X | X = X
For binary math operations,
- multiply or divide Try to decompose one binary number into a sum of single bit on numbers so that the left shift operation can be used.
3 * 10
= 0011 * 1010
= 0011 * ( 1000 + 0010)
= (0011 * 1000) + (0011 * 0010 )
= ( 0011 << 3) + ( 0011 << 1)
= ( 0001 1000 ) + 0110
= 24 + 6
= 30
a = XOR(a, b) // difference b = XOR(b, a) // get the original a a = XOR(a, b) // get the original b
Two's Complement and Negative Numbers
Two's complement is a mathematical operation on binary numbers.
The two's complement of an N-bit number is defined as its complement with respect to 2 exp(N). For instance, for the three-bit number 010, the two's complement is 110, because 010 + 110 = 1000.
It is calculated by inverting the digits and adding one.
In computer, a positive number is represented as itself while a negative number is represented as the two's complement of its absolute value.
If the binary number 010 encodes the signed integer 2, then its two's complement, 110, encodes the inverse: −2.
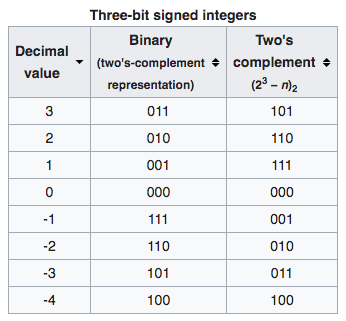
Arithmetic vs. Logical Right Shift
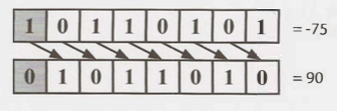
In a logical right shift, we shift the bits and put a 0 in the most significant bit. It is indicated with a >>> operator. The MSB is not reserved after logical shift.
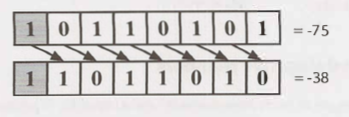
In a arithmetic right shift , the MSB is filled with the value of the previous.
The following code print "-16 right shifted: -8".
int num=-16;
printf("%d right shifted: %d\n", num, (num >>1));
The >> operator in C and C++ is not necessarily an arithmetic shift:
- it is only an arithmetic shift if used with a signed integer type
- If it is used on an unsigned integer type instead, it will be a logical shift.
Common Bit Tasks: Getting and Setting
- Get Bit
bool getBit(int num, int bitNo){
return ( (num & ( 1 << bitNo )) != 0 );
}
int setBit((int num, int bitNo){
return ( num | ( 1 << bitNo ) );
}
int clearBit(int num, int bitNo){
int mask = ~( 1 << bitNo );
return ( num & mask );
}
int clearBitsFromMSB(int num, int bitNo){
int mask = ( 1 << bitNo ) - 1;
return ( num & mask );
}
int clearBitsFromBit(int num, int bitNo){
int mask = (-1 << (bitNo + 1));
return ( num & mask );
}
int updateBit(int num, int bitNo, bool value){
int mask = ~( 1 << bitNo );
return ( num & mask ) | (value << i);;
}
Chapter 6 Math and Logic Puzzles
Prime Numbers
- Checking for Primality
- the naive way
boolean primeNaive(int n) {
if(n<2){
return false;
}
for (int i= 2; i < n; i++) {// except 1
if (n % i == 0) {// divide by any number less than itself
return false;
}
}
}
boolean primeSlightlyBetter(int n) {
if (n < 2) {
return false;
}
int sqrt= (int) Math.sqrt(n);
for (int i= 2; i < sqrt; i++) {// except 1
if (n % i == 0) {// divide by any number less than itself
return false;
}
}
}
- 列出所有小於開根號的數
- 第一個質數是2
- 可被質數整除的數(質數的倍數)就不是質數.
- 找出下一個質數, 重複以上步驟
def eratosthenes(n):
IsPrime = [True] * (n + 1)
for i in range(2, int(n ** 0.5) + 1): // prime's range <= sqrt(n)
if IsPrime[i]:
for j in range(i * i, n + 1, i): // exclude this prime's multiples between (i*i) and (n+1)
IsPrime[j] = False
return [x for x in range(2, n + 1) if IsPrime[x]]
if __name__ == "__main__":
print(eratosthenes(120))
C:
boolean[] sieveOfEratosthenes(int max) {
boolean[] flags= new boolean[max + 1];
int count= 0;
init(flags); // Set all flags to t rue other than 0 and 1
int prime = 2;
while ( prime <= Math.sqrt(max) ) {
/* Cross off remaining multiples of prime */
crossOff(flags, prime);
/* Find next value which is true */
prime = getNextPrime(flags, prime);
}
return flags;
}
void crossOff(boolean[] flags, int prime) {
/* Cross off remaining multiples of prime. We can start with (prime*prime),
* because if we have a k * prime, where k < prime, this value would have
* already been crossed off in a prior iteration. */
for (int i= prime * prime; i < flags.length; i += prime) {
flags[i] = false;
}
}
int getNextPrime(boolean[] flags, int prime) {
int next = prime + 1;
while (next < flags.length && !flags[next]) {
next++;
}
return next;
}
Probability
- Bayes' Theorem and Conditional Probability For a joint probability distribution over events A and B, P(A ∩ B), the conditional probability of A given B is defined as
P(A | B) = P(A∩B) / P(B)
Chapter 7 Object-Oriented Design
This requires a candidate to sketch out the classes and methods to implement technical problems or real-life objects. They are about demonstrating that you understand how to create elegant, maintainable object-oriented code.How to Approach
The following approach will work well for many problems.- Handle Ambiguity You should inquire who is going to use it and how they are going to use it.
- Define the core objects
- Analyze relationships Which objects are members of which other objects? Do any objects inherit from any others? Are relationships many-to-many or one-to-many?
- Investigate Actions Consider the key actions that the objects will take and how they relate to each other.
- Design Patterns
- Singleton Class A class has only one instance and ensures access to the instance through the application. It can be useful in cases where you have a "global" object with exactly one instance.
- Factory Method The Factory Method offers an interface for creating an instance of a class, with its subclasses deciding which class to instantiate.
Chapter 8 Recursion and Dynamic Programming
Dynamic Programming is mainly an optimization over plain recursion.
A good hint that a problem is recursive is that it can be built off of subproblems.
How to Approach
There are many ways you might divide a problem into subproblems. Three of the most common approaches to develop an algorithm are:- bottom-up
- top-down
- half-and-half
Recursive vs. Iterative Solutions
Recursive algorithms can be very space inefficient. Each recursive call adds a new layer to the stack, which means that if your algorithm recurses to a depth of n, it uses at least O(n) memory. For this reason, it's often better to implement a recursive algorithm iteratively. All recursive algorithms can be implemented iteratively .Dynamic Programming & Memoization
Dynamic Programming is mainly an optimization over plain recursion. Wherever we see a recursive solution that has repeated calls for same inputs, we can optimize it using Dynamic Programming. The idea is to simply store the results of subproblems, so that we do not have to re-compute them when needed later. This simple optimization reduces time complexities from exponential to polynomial. For example, if we write simple recursive solution for Fibonacci Numbers,
//Fibonacci Series using Recursion
#include <stdio.h>
int fib(int n)
{
if (n <= 1)
return n;
return fib(n-1) + fib(n-2);
}
we get exponential time complexity:
T(n) = T(n-1) + T(n-2)
fib(5)
/ \
fib(4) fib(3)
/ \ / \
fib(3) fib(2) fib(2) fib(1)
/ \ / \ / \
fib(2) fib(1) fib(1) fib(0) fib(1) fib(0)
/ \
fib(1) fib(0)
If we optimize it by storing solutions of subproblems, time complexity reduces to linear.
//Fibonacci Series using Dynamic Programming
#include <stdio.h>
int fib(int n)
{
/* Declare an array to store Fibonacci numbers. */
int f[n+2]; // 1 extra to handle case, n = 0
int i;
/* 0th and 1st number of the series are 0 and 1*/
f[0] = 0;
f[1] = 1;
for (i = 2; i <= n; i++)
{
/* Add the previous 2 numbers in the series
and store it */
f[i] = f[i-1] + f[i-2];
}
return f[n];
}
We can optimize the space used in method 2 by storing the previous two numbers only
// Fibonacci Series using Space Optimized Method
#include <stdio.h>
int fib(int n)
{
int a = 0, b = 1, c, i;
if( n == 0)
return a;
for (i = 2; i <= n; i++)
{
c = a + b;
a = b;
b = c;
}
return b;
}
Chapter 9 System Design and Scalability
If you were asked by your manager to design some system, what would you do? Tackle the problem by doing it just like you would at work. Ask questions. Engage the interviewer. Discuss the tradeoffs.Chapter 10 Sorting and Searching
Common Sorting Algorithms
- Bubble Sort Runtime: O( n*n ) average and worst case. Memory: O( 1). 它重複地走訪過要排序的數列,一次比較兩個元素,如果他們的順序錯誤就把他們交換過來。 這個算法的名字由來是因為越小的元素會經由交換慢慢「浮」到數列的頂端。 Example:
- First Pass:
( 5 1 4 2 8 ) –> ( 1 5 4 2 8 ), Here, algorithm compares the first two elements, and swaps since 5 > 1. ( 1 5 4 2 8 ) –> ( 1 4 5 2 8 ), Swap since 5 > 4 ( 1 4 5 2 8 ) –> ( 1 4 2 5 8 ), Swap since 5 > 2 ( 1 4 2 5 8 ) –> ( 1 4 2 5 8 ), Now, since these elements are already in order (8 > 5), algorithm does not swap them.
( 1 4 2 5 8 ) –> ( 1 4 2 5 8 ) ( 1 4 2 5 8 ) –> ( 1 2 4 5 8 ), Swap since 4 > 2 ( 1 2 4 5 8 ) –> ( 1 2 4 5 8 ) ( 1 2 4 5 8 ) –> ( 1 2 4 5 8 ) Now, the array is already sorted, but our algorithm does not know if it is completed. The algorithm needs one whole pass without any swap to know it is sorted.
( 1 2 4 5 8 ) –> ( 1 2 4 5 8 ) ( 1 2 4 5 8 ) –> ( 1 2 4 5 8 ) ( 1 2 4 5 8 ) –> ( 1 2 4 5 8 ) ( 1 2 4 5 8 ) –> ( 1 2 4 5 8 )
// A function to implement bubble sort
void bubbleSort(int arr[], int n)
{
int i, j;
for (i = 0; i < n-1; i++) // times of pass
// The first i elements are already been put in correct position from the end
for (j = 0; j < n-i-1; j++)
if (arr[j] > arr[j+1])
swap(&arr[j], &arr[j+1]);
}
void selection_sort(int arr[], int len)
{
int i,j;
for (i = 0 ; i < len - 1 ; i++) {
int min = i;
for (j = i + 1; j < len; j++) { //走訪未排序的元素
if (arr[j] < arr[min]) //找到目前最小值
min = j; //紀錄最小值
}
swap(&arr[min], &arr[i]); //做交換
}
}
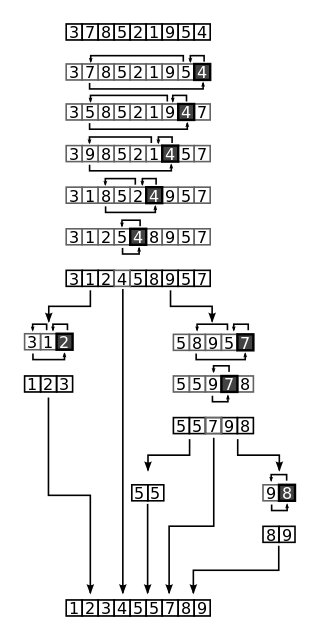
mergeSort(arr[], l, r)
If r > l
1. Find the middle point to divide the array into two halves:
middle m = (l+r)/2
2. Call mergeSort for first half:
Call mergeSort(arr, l, m)
3. Call mergeSort for second half:
Call mergeSort(arr, m+1, r)
4. Merge the two halves sorted in step 2 and 3:
Call merge(arr, l, m, r)

- Pick an element, called a pivot, from the array.
- Partitioning: reorder the pivot's position so that all elements with values less than the pivot come before the pivot, while all elements with values greater than the pivot come after it (equal values can go either way). After this partitioning, the pivot is in its final position. This is called the partition operation.
- Recursively apply the above steps to the sub-array of elements with smaller values and separately to the sub-array of elements with greater values.
 There can be many ways to do partition, following pseudo code pick the last element as the pivot point:
There can be many ways to do partition, following pseudo code pick the last element as the pivot point:
/* low --> Starting index, high --> Ending index */
quickSort(arr[], low, high)
{
if (low < high)
{
/* pi is partitioning index, arr[pi] is now
at right place */
pi = partition(arr, low, high);
quickSort(arr, low, pi - 1); // Before pi
quickSort(arr, pi + 1, high); // After pi
}
}
/* This function takes last element as pivot, places
the pivot element at its correct position in sorted
array, and places all smaller (smaller than pivot)
to left of pivot and all greater elements to right
of pivot */
int partition (arr[], low, high)
{
// pivot (Element to be placed at right position)
pivot = arr[high];
i = (low - 1) // Index of the nearest smaller element to the pivot
for (j = low; j <= high- 1; j++)
{
// If current element is smaller than or equal to pivot
if (arr[j] <= pivot) // swap and append the smaller element
{
// increment index of smaller element which is nearest to the pivot
i++;
// j is always >= i, move the smaller element to the right
swap arr[i] and arr[j]
}
}
// after all smaller elements are swapped before the pivot
swap arr[i + 1] and arr[high]) // swap the pivot
return (i + 1) // return the index of the pivot
}
Radix Sort
The lower bound for Comparison based sorting algorithm (Merge Sort, Heap Sort, Quick-Sort .. etc) is O(n Log(n) ).Radix sort is a non-comparative integer sorting algorithm , it was developed to sort large integers. As integer is treated as a string of digits so we can also call it as string sorting algorithm.
基數(radix)排序的方式可以採用LSD(Least significant digital)或MSD(Most significant digital),LSD的排序方式由鍵值的最右邊開始,而MSD則相反,由鍵值的最左邊開始。
採用LSD: 先從低位排序

Assume a list has n entries and each entry is a decimal key .
#include <stdio.h>
#define MAX 20 // the max. acceptable input entries
//#define SHOWPASS
#define BASE 10
void print(int *a, int n) {
int i;
for (i = 0; i < n; i++) {
printf("%d\t", a[i]);
}
}
void radixsort(int *a, int n) {
int i, b[MAX], m = a[0], exp = 1;
// find the max. value of input entries
for (i = 1; i < n; i++) {
if (a[i] > m) {
m = a[i];
}
}
while (m / exp > 0) { // until the all digits in the max. value are processed
// reset bucket for a digit
// bucket is an array store the count for each radix value
int bucket[BASE] = { 0 };
// count for radix values used in this digit
for (i = 0; i < n; i++) {
bucket[(a[i] / exp) % BASE]++;
}
// accumulated count for the values used in this digit
for (i = 1; i < BASE; i++) {
bucket[i] += bucket[i - 1];
}
for (i = n - 1; i >= 0; i--) { // process from the last ordered sequence a[i]
// find the digit value for an entry
// save the entry in b[] with the index in the range reserved for the same digital value
b[--bucket[(a[i] / exp) % BASE]] = a[i];
}
for (i = 0; i < n; i++) {
a[i] = b[i];
}
exp *= BASE;
#ifdef SHOWPASS
printf("\nPASS : ");
print(a, n);
#endif
}
}
int main() {
int arr[MAX];
int i, n;
printf("Enter total elements (n <= %d) : ", MAX);
scanf("%d", &n);
n = n < MAX ? n : MAX;
printf("Enter %d Elements : ", n);
for (i = 0; i < n; i++) {
scanf("%d", &arr[i]);
}
printf("\nARRAY : ");
print(&arr[0], n);
radixsort(&arr[0], n);
printf("\nSORTED : ");
print(&arr[0], n);
printf("\n");
return 0;
}
Search Algorithms
Binary Search是一種在sorted array中尋找某一特定元素的搜尋演算法。By comparing x to the midpoint of the array:
- If x is less than the midpoint, then we search the left half of the array.
- If x is greater than the midpoint, then we search the right half of the array.
- We repeat the above process until we either find x or the subarray has size 0.
- Recursive
int binary_search(const int arr[], int start, int end, int khey) {
if (start > end)
return -1;
int mid = start + (end - start) / 2; //直接平均可能會溢位,所以用此算法
if (arr[mid] > khey)
return binary_search(arr, start, mid - 1, khey);
else if (arr[mid] < khey)
return binary_search(arr, mid + 1, end, khey);
else
return mid; //最後檢測相等是因為多數搜尋狀況不是大於要不就小於
}
int binary_search(const int arr[], int start, int end, int key) {
int ret = -1; // 未搜索到数据返回-1下标
int mid;
while (start <= end) {
mid = start + (end - start) / 2; //直接平均可能會溢位,所以用此算法
if (arr[mid] < key)
start = mid + 1;
else if (arr[mid] > key)
end = mid - 1;
else { // 最後檢測相等是因為多數搜尋狀況不是大於要不就小於
ret = mid;
break;
}
}
return ret; // 单一出口
}
Chapter 11 Testing
Chapter 12 C and C++
Basic C++ syntax.
Classes and Inheritance
Here’s a simple class to represent a generic person:
#include <string>
class Person
{
public:
std::string m_name;
int m_age;
Person(std::string name = "", int age = 0)
: m_name(name), m_age(age)
{
}
std::string getName() const { return m_name; }
int getAge() const { return m_age; }
};
All data members and methods are private by default in C++.One can modify this by introducing the keyword public.
in this example, all generic variables and functions are declared as public.
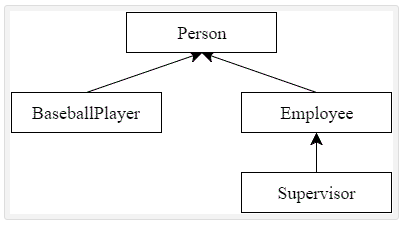
To have BaseballPlayer inherit from our Person class,
// BaseballPlayer publicly inheriting Person
class BaseballPlayer : public Person
{
public:
double m_battingAverage;
int m_homeRuns;
BaseballPlayer(double battingAverage = 0.0, int homeRuns = 0)
: m_battingAverage(battingAverage), m_homeRuns(homeRuns)
{
}
};
When BaseballPlayer inherits from Person, BaseballPlayer acquires the member functions and variables from Person.Additionally, BaseballPlayer defines two members of its own: m_battingAverage and m_homeRuns.
Now let’s write another class that also inherits from Person.
// Employee publicly inherits from Person
class Employee: public Person
{
public:
double m_hourlySalary;
long m_employeeID;
Employee(double hourlySalary = 0.0, long employeeID = 0)
: m_hourlySalary(hourlySalary), m_employeeID(employeeID)
{
}
void printNameAndSalary() const
{
std::cout << m_name << ": " << m_hourlySalary << '\n';
}
};
It’s possible to inherit from a class that is itself derived from another class.
class Supervisor: public Employee
{
public:
// This Supervisor can oversee a max of 5 employees
long m_overseesIDs[5];
Supervisor()
{
}
};
Constructors and Destructors
The constructor of a class is automatically called upon an object's creation.If no constructor is defined, the compiler automatically generates one called the Default Constructor.
Initializer List is used in initializing the data members of a class. The list of members to be initialized is indicated with constructor as a comma-separated list followed by a colon.
Following is an example that uses the initializer list to initialize x and y of Point class.
#include <iostream>
using namespace std;
class Point {
private:
int x;
int y;
public:
Point(int i = 0, int j = 0):x(i), y(j) {}
/* The above use of Initializer list is optional as the
constructor can also be written as:
Point(int i = 0, int j = 0) {
x = i;
y = j;
}
*/
int getX() const {return x;}
int getY() const {return y;}
};
int main() {
Point t1(10, 15);
cout<<"x = "<<t1.getX()<<", ";
cout<<"y = "<<t1.getY();
return 0;
}
/* OUTPUT:
x = 10, y = 15
*/
The destructor cleans up upon object deletion and is automatically called when an object is destroyed.It cannot take an argument as we don't explicitly call a destructor.
Virtual Functions
class Person {
int id; // all members are private by default
char name[NAME_SIZE];
public:
void aboutMe() {
cout « "I am a person.";
}
} ;
class Student : public Person {
public:
void aboutMe() {
cout << "I am a student.";
};
}
Student * p1 = new Student();
p1->aboutMe(); // I am a student.
Person * p = new Student();
p->aboutMe(); // "I am a person."
This is because the function aboutMe() is resolved at compile-time, in a mechanism known as static binding.The virtual specifier specifies that a non-static member function is virtual and supports dynamic dispatch.
If we want to ensure that the Student's implementation of aboutMe() is called, we can define aboutMe() in the Person class to be virtual.
class Person {
...
virtual void aboutMe() {
cout << "I am a person.";
}
};
An abstract class is, conceptually, a class that cannot be instantiated and is usually implemented as a class that has one or more pure virtual (abstract) functions.
class AbstractClass {
public:
virtual void AbstractMemberFunction() = 0; // Pure virtual function makes
// this class Abstract class.
virtual void NonAbstractMemberFunction1(); // Virtual function.
void NonAbstractMemberFunction2();
};
It's a way of forcing a contract between the class designer and the users of that class.
If we wish to create a concrete class (a class that can be instantiated) from an abstract class, we must declare and define a matching member function for each abstract member function of the base class. Otherwise, if any member function of the base class is left undefined, we will create a new abstract class (this could be useful sometimes).
Virtual Destructor
Making base class destructor virtual guarantees that the object of derived class is destructed properly, i.e., both base class and derived class destructors are called. For example,
// A program with virtual destructor
#include<iostream>
using namespace std;
class base {
public:
base()
{ cout<<"Constructing base \n"; }
virtual ~base()
{ cout<<"Destructing base \n"; }
};
class derived: public base {
public:
derived()
{ cout<<"Constructing derived \n"; }
~derived()
{ cout<<"Destructing derived \n"; }
};
int main(void)
{
derived *d = new derived();
base *b = d;
delete b;
getchar();
return 0;
}
Constructing base
Constructing derived
Destructing derived
Destructing base
Default Values
Functions can specify default values, as shown below. Note that all default parameters must be on the right side of the function declaration, as there would be no other way to specify how the parameters line up.
int func(int a, int b = 3) {
X = a;
y = b;
return a + b;
}
w = func(4);
z = func(4, 5);
Operator Overloading
In C++, we can make operators to work for user defined classes. This means C++ has the ability to provide the operators with a special meaning for a data type, this ability is known as operator overloading.
For ex., we could overload the + operator for complex bumbers as follows.
#include
using namespace std;
class Complex {
private:
int real, imag;
public:
Complex(int r = 0, int i =0) {real = r; imag = i;}
// This is automatically called when '+' is used with
// between two Complex objects
Complex operator+ (Complex const &obj) {
Complex res;
res.real = real + obj.real;
res.imag = imag + obj.imag;
return res;
}
void print() { cout << real << " + i" << imag << endl; }
};
int main()
{
Complex c1(10, 5), c2(2, 4);
Complex c3 = c1 + c2; // An example call to "operator+"
c3.print();
}
12 + i9
Pointers and References
A pointer holds the address of a variable and can be used to perform any operation that could be directly done on the variable, such as accessing and modifying it.
Two pointers can equal each other, such that changing one's value also changes the other's value (since they, in fact, point to the same address).
int * p = new int;
*p = 7;
int * q = p;
*p = 8;
cout « *q; // prints 8
When a variable is declared as reference, it becomes an alternative name for an existing variable.
A variable can be declared as reference by putting ‘&’ in the declaration.
A reference is another name (an alias) for a pre-existing object and it does not have memory of its own. For example:
#include<iostream>
using namespace std;
int main()
{
int x = 10;
// ref is a reference to x.
int& ref = x;
// Value of x is now changed to 20
ref = 20;
cout << "x = " << x << endl ;
// Value of x is now changed to 30
x = 30;
cout << "ref = " << ref << endl ;
return 0;
}
Performing p++ will skip ahead by bytes which is the size of the data structure the pointer points to.
Templates
A template is a simple and yet very powerful tool in C++.
The simple idea is to pass data type as a parameter so that we don’t need to write the same code for different data types.
C++ adds two new keywords to support templates: ‘template’ and ‘typename’. The second keyword can always be replaced by keyword ‘class’.
Templates are expanded at compiler time. This is like macros.
The difference is, compiler does type checking before template expansion. The idea is simple, source code contains only function/class, but compiled code may contain multiple copies of same function/class.

- Function Templates We write a generic function that can be used for different data types.
#include <iostream>
using namespace std;
// One function works for all data types. This would work
// even for user defined types if operator '>' is overloaded
template <typename T>
T myMax(T x, T y)
{
return (x > y)? x: y;
}
int main()
{
cout << myMax(3, 7) << endl; // Call myMax for int
cout << myMax(3.0, 7.0) << endl; // call myMax for double
cout << myMax('g', 'e') << endl; // call myMax for char
return 0;
}
#include <iostream>
using namespace std;
template <typename T>
class Array {
private:
T *ptr;
int size;
public:
Array(T arr[], int s);
void print();
};
template <typename T>
Array<T>::Array(T arr[], int s) {
ptr = new T[s];
size = s;
for(int i = 0; i < size; i++)
ptr[i] = arr[i];
}
template <typename T>
void Array<T>::print() {
for (int i = 0; i < size; i++)
cout<<" "<<*(ptr + i);
cout<<endl;
}
int main() {
int arr[5] = {1, 2, 3, 4, 5};
Array<int> a(arr, 5);
a.print();
return 0;
}
Chapter 13 Java
Chapter 14 Database
Chapter 15 Threads and Locks
Chapter 16 Moderate
Chapter 17 Hard
References
- Grokking the Coding Interview
- Grokking the System Design Interview
- Grokking the Object Oriented Design Interview
Introduction to the volatile keyword
The volatile keyword indicates that a value may change between different accesses, even if it does not appear to be modified. This keyword prevents an optimizing compiler from optimizing away subsequent reads or writes.
A variable should be declared volatile whenever its value could change unexpectedly. In practice, only three types of variables could change:
- Memory-mapped peripheral registers
- Global variables modified by an interrupt service routine
- Global variables within a multi-threaded application
Example of memory-mapped I/O in C,
static int foo;
void bar(void) {
foo = 0;
while (foo != 255)
;
}
void bar_optimized(void) {
foo = 0;
while (true)
;
}
To prevent the compiler from optimizing code as above, the volatile keyword is used:
static volatile int foo;
void bar (void) {
foo = 0;
while (foo != 255)
;
}
Memory Layout of Executable Programs
A typical memory representation of C program consists of following sections.
- Text segment This contains executable instructions.
- Initialized data segment This contains the global and static variables that are initialized by the programmer.
- Uninitialized data segment This is often called the “bss” segment, “block started by symbol”, this contains all global static variables that are initialized to zero or do not have explicit initialization in source code.
- Stack The stack area contains the program stack, a LIFO structure. . A “stack pointer” register tracks the top of the stack; it is adjusted each time a value is “pushed” onto the stack. The set of values pushed for one function call is termed a “stack frame”; A stack frame consists at minimum of a return address. Stack saves information each time a function is called, including automatic variables (local variables) which are allocated and free while entering and leaving the function.
- Heap Heap is the segment where dynamic memory allocation usually takes place. Heap area is managed by malloc(), realloc(), and free() The Heap area is shared by all shared libraries and dynamically loaded modules in a process.
Examples,
#include <stdio.h>
int main(void)
{
return 0;
}
$ gcc memory-layout.c -o memory-layout
$ size memory-layout
text data bss dec hex filename
1415 544 8 1967 7af test
- add one global variable in program, now check the size of bss
#include <stdio.h>
int global; /* Uninitialized variable stored in bss*/
int main(void)
{
return 0;
}
$ gcc memory-layout.c -o memory-layout
$ size memory-layout
text data bss dec hex filename
1415 544 8 1967 7af test
#include <stdio.h>
int main(void)
{
int i=0, j=0, k=0, l=0, m=0, n=0;
return 0;
}
$ gcc memory-layout.c -o memory-layout
$ size memory-layout
text data bss dec hex filename
1447 544 8 1999 7cf test
#include <stdio.h>
int global; /* Uninitialized variable stored in bss*/
int main(void)
{
static int i; /* Uninitialized static variable +4 bytes in bss */
return 0;
}
$ gcc memory-layout.c -o memory-layout
$ size memory-layout
text data bss dec hex filename
1415 544 16 1975 7b7 test
#include <stdio.h>
int global; /* Uninitialized variable stored in bss*/
int main(void)
{
static int i = 100; /* Initialized static variable +4 bytes in .data */
return 0;
}
$ gcc memory-layout.c -o memory-layout
$ size memory-layout
text data bss dec hex filename
1415 548 12 1975 7b7 test
#includeint global = 10; /* initialized global +4 bytes in .data*/ int main(void) { static int i = 100; /* Initialized static variable stored in DS*/ return 0; } $ gcc memory-layout.c -o memory-layout $ size memory-layout text data bss dec hex filename 1415 552 8 1975 7b7 test
Interview Questions
What are some “trick questions” in job interviews and how should applicants deal with them?
Question: Why did you leave your previous job?
What I’m really looking for: I’m looking for you to reveal what it’s like to work with you, because when we speak about others we are really talking about ourselves.
How to handle it: Say something honest that speaks to the future, such as “I was ready for the next opportunity”.
What not to say: Never complain or criticize the place where you used to work, or anyone you used to work for.
Question: What are you looking for in your next opportunity?
What I’m really looking for: I want to confirm that what you want matches what I am offering. I want us to be compatible.
How to handle it: Make sure you study the company and the job description and go in with clarity regarding what they want to find. You too should be looking for the best possible fit.
What not to say: Anything that reveals a lack of connection between the company I am working for and the person I am interviewing. “I just really need a job” might be honest, but it doesn’t help me determine why you are the best candidate for the job.
Question: Tell me about you.
What I’m really looking for: I am looking for a quick summary of your work history, but I’m also looking to see what you highlight. Ideally, what you speak about with the most enthusiasm is what I need the most.
How to handle it: Make the answer as specific, focused and short as possible and ask a question back. “I have been working in the communications industry for 20 years and am curious to know what the ideal candidate looks like for you, which would provide context for what I want to tell you more about”. Turn it into a conversation.
What not to say: Do not use catch phrases. “I am a go-getter”. Do not launch into a detailed laundry list of all the things you have done. Long answers result in people tuning you out.
Question: What is your biggest weakness?
What I’m really looking for: Everyone has weaknesses. I want to know if yours are compatible with my candidate search. For example, if the job is to lead a team thoughtfully, I don’t want to hear you’d rather make a bad decision than no decision.
How to handle it: Do your homework, then be honest with a weakness that you really struggle with. “I am enthusiastic in finding the root cause and as such sometimes struggle to prioritize”.
Being honest with a weakness means you end up in a job that is right for you.
What not to say: Please don’t say “I’m a perfectionist”. Perfectionists are reluctant to try new things and as such don’t grow as quickly as people who are less afraid to fail.
Question: Give me an example of a mistake you made and how you fixed it.
What I’m really looking for: Everyone makes mistakes. I want to know if you are self-aware and coachable. I want to see if you have courage and accountability or if you place blame on others.
How to handle it: State a mistake, own up to it, then explain how you found a solution. The whole answer should be both clear and brief.
What not to say: “I never make mistakes. And I never would have made this one if it hadn’t been for my boss, who consistently used me to cover his own ass.”
Question: What salary are you looking for?
What I’m really looking for: I really want to know how much you want to see if under my budget limitations I can afford you.
How to handle it: Choose a range that’s fair and that would make you happy for the next 365 days.
What not to say: Candidates who answer this question clearly are always taken more seriously than those who refuse to answer.
Question: Where do you see yourself in 5 years?
What I’m really looking for: I want to know if you are a long-term player. Attrition hurts my business.
How to handle it (if you don’t have a 5 year plan): “I am looking for a position where I can ideally grow within the company. In 5 years I hope to be learning and growing.”
What not to say: “I don’t know.” It’s OK not to know, but it doesn’t help distinguish you from other candidates.
Question: Why should you get this job?
What I’m really looking for: A top line summary of your strengths and how clearly you deliver them.
How to handle it: Rehearse. Have this answer ready. The general message should be “the attributes you are looking for match my natural strengths, and my track record proves this.”
What not to say: Something that reflects you’re thinking about yourself and not the company. “Because I am the best” is less impressive than “because I know how to contribute to the company exceeding business objectives”.
Bonus tip:
Once a company determines they want to hire you they will ask for references. Don’t just give them the contact information: follow through. Call your references and say “This company is specifically looking for someone to lead their team. I would really appreciate it if you could highlight the work we did when I lead xx project, and how I handled making sure everyone felt listened to”.
2021 疫情找工作-面試分享 Google/MS/Amazon/Roku
- 6. Microsoft — Sr. Software Engineer
我面試的是微軟的 Device Team,目前主要產品是 Android 手機 Surface Duo,其實這個團隊主力是微軟併購 Movial 來的,所以對於在微軟做 Android 這件事就沒有很意外了。這次面試是微軟的 Recruiter 從 LinkedIn 主動聯繫。 面試流程:五關 (兩關中文三關英文 各 45 mins) -> offer 第一關 Coding test:寫了三題 LeetCode ,難度介於 Easy-Medium,涵蓋了 主要的資料結構 Linked List/Tree/Stack/Queue 等等。 第二關 Android questions:先從履歷中跟 Android Framework 比較相關的地方開始問起,懂 Window Manager 和 Activity Manager 會比較吃香,我這邊比較吃虧這兩塊都不是熟悉的領域,後來面試官還說:我怎麼覺得 BSP team 比較適合你 XD。 第三關第四關非常像:先問了一輪履歷經驗,再帶出一些 behavior questions,最後說來寫個 coding 吧,第三關出了一道 Linked List,第四關出了一題 Stack + follow up,都不難大概是 LeetCode Easy-Medium 等級。 第五關有點偏 system design,困難點在於直接把 Surface Duo 可能遇到的問題拿出來討論,像是雙螢幕 UI 交互的一些情境,如果有對這個產品下過功夫研究應該可以答的更好,我是回答得有點吃力啦,一來是對這產品真的沒有很熟,二來是英文沒有好的可以流暢的邊想邊回答,雖然最後拿到 positive feedback,但過程中真的汗流浹背。 結果:offer get. 薪資一線水準。
Pixel team。朋友內推
- Coding Quiz The first step is clearing an online assessment test which is usually a coding quiz you must complete within 90 minutes.
- Phone Screen Phone or video conversations with the recruiters or a peer on the team, lasting 30-60 minutes.
- Arrays, Strings, and Linked Lists
- Graph Algorithms, including Greedy Algorithms
- Hash Tables and Queues
- Recursion
- Sorting Algorithms — Quicksort, Merge Sort, Heap Sort, etc.
- Trees and Graphs
- Dynamic Programming
- On-site All the questions are open-ended because the hiring managers want to learn more about your problem-solving approach and how your mind works. Google also follows structured interviewing, which means that every candidate is evaluated on the same framework. Whiteboard and coding challenges are common during this round.
- 第一關 Coding test: LeetCode Bit Manipulation 變形題。
- 第二關 Embedded System Coding: ISR/Lock/Multi-threading 相關實作細節
- 第三關 Domain knowledge + Coding:Domain knowledge 問得很深,會根據你的回答再繼續追問細節。最後考了一題 LeetCode 沒看過的 string parsing 問題。
- 第四關 Behavior questions:討論一些工作上會遇到的情境,主要看你遇到一些困難的時候會用什麼方式應對,也提到跟不同時區團隊合作時需要大清早或深夜工作的情況。
- 第五關 Coding test:考了一題二維空間比大小,印象中 LeetCode 有看過類似但細節不同的問題。
- 第六關 Domain knowledge + Linux kernel questions:問了蠻多作業系統相關的細節,還好面試前有乖乖去複習過一遍 OS,大致都答的出來。
During this round, the interviewers are keen to know everything on your resume and ask you a coding question that you need to explain in a Google Doc.
In other words, they want to know if you have the key skills needed for the role.
Recommended Reading: Google Phone Screen Interview Questions
Below is a list of topics to prepare for the phone screen interview:
Recommended Reading: How to Prepare for Google's Onsite Interview
面試流程:六關 (五關中文一關英文 各 45 mins):
面試流程:OA -> phone screen (中文 1 hr) -> on-site 四關 (全中文 各 1 hr) -> Candidate Chat -> 加面一關 SysDE -> offer
- Online Assessment Prepare for the experience by taking this sample coding challenge.
- Phone Screen 由 Hiring Manager 面試,主要是討論履歷做過的案子,也分享了一下 Sidewalk team 目前的規劃及未來目標。
- On-site Software Development Engineer Interview Preparation:(video)
- Amazon Leadership Principles
- Amazon Coding Sample
- Amazon System Design Preparation
- SDE Interview FAQs
- SDE Interview Coding Example
- 第一關 30 mins behavior questions + 30 mins coding。前面 behavior questions 因為有所準備,當下要套入哪個 14 leadership principles 都還回答的蠻順利的。
- 第二關 30 mins behavior questions + 30 mins system design。
- 第三關 behavior + embedded system + coding。這場除了老樣子 behavior questions (14 leadership principles!!) 之外,問了比較多 embedded linux 相關的 domain knowledge,像是 Booting sequence、memory layout、ISR 等等,最後剩十多分鐘忽然說還是來寫個 coding 吧,就出了一題計算 time interval overlap,難度應該是 LeetCode Medium,這題因為下一場面試時間直接接在後面,剩十幾分鐘實在太趕,一開始方向不對就很難完成,最後有些部分只能用註解跟口述解釋我的作法。
- 第四關 behavior + coding。因為 onsite 是連續的面試,面到這場已經有點精神疲憊。Coding 題目跟 string encode/decode 有關,當下只能寫出一個非最佳解,看得出來面試官沒有很滿意,過程中大概也知道他希望的解法是什麼,但最後就有種氣力放盡的感覺 XD,有被連續面試轟炸過的人應該可以體會。
- Candidate Chat 這場半小時是不計入面試評分的,由一位非常資深的 Amazon 大主管來跟你聊聊公司團隊工作等等,事後去搜尋了一下資歷相當驚人呀,我覺得這場還不錯,有一種被重視的感覺。
用 HackerRank 寫兩題 135 分鐘,除了寫程式以外還要用一個篇幅解釋你的想法,外加 15 分鐘的 work style questions。
我覺得重點都不是在考演算法,而是細心和 edge case,我第一題測資 15/16 pass,第二題 11/16 pass,都沒有全過,當下想說慘了 OA 就要爆了,結果幸運的進到下一關 phone screen。
也很感謝有特別提醒我 Amazon 非常注重 behavior questions,14 leadership principles 更是面試必問,讓我有所準備,不然後面幾關應該會被問倒。
Coding 部分出了一個棋牌遊戲,要你從 class 設計開始一直寫到某個指定的功能,我覺得時間有點太趕,前面還花了幾分鐘讀懂遊戲規則,最後硬寫了一個效能不好的版本出來。
System design 方面是設計一套 IOT 警示系統,從硬體、網路、雲端各種架構去思考這套系統,並討論不同情境底下的 trade off。關於 System Design 這方面比較沒有特別去準備,所以就以自己的經驗去提出第一個版本,再根據面試官的問題去修正。
面試流程:OA -> phone screen (英文 1.5 hrs)-> on-site 五關 (全英文 各 1 hr) -> offer
- Online Assessment 用 HackerRank 寫三題 60 分鐘,題目涵蓋 Bit Manipulation/Sort/String/Array,我覺得題目相對來說不難,大概 45 分鐘寫完測資全過,花五分鐘整理一下 code 就交卷。
- Phone Screen 花了一些時間討論履歷做過的案子以及一些 embedded system 相關的問題,然後考了一題 min/max grouping,寫了一兩個解法面試官覺得 ok,但問我有沒有更快的解法,我想了一個 DP 解但卡住寫不完,面試官最後說沒關係不用這麼複雜,還分享了一個不用 DP 但比較快的解法。
- On-site
- 第一關 問了一堆 C++ 語法,static/extern/virtual function/shared_ptr 還有各種繼承問題等等,然後考了一題 hashmap,測資全過。
- 第二關 問了蠻多 embedded system 相關的問題,考了一題 group division,也是測資全過。
- 第三關 也是問履歷及 embedded system 相關的問題,考了一題 LeetCode Easy 等級的,測資全過。
- 第四關 一位英國人面試官,主要問 Behavior questions 以及介紹 Roku 的歷史、團隊及未來發展,也提到 Roku 現在正在大幅擴張階段,收了很多不同國家的人又要同時保存公司文化,是一個挑戰。
- 第五關 面試官是一個很嗨的大叔,但口音有點重,有時候真的聽不太懂他在說什麼,考了兩題 Coding,是那種 math trick 題,因為他很嗨會邊講邊大笑,所以光理解題目就花了好一番功夫,我覺得寫的不怎麼樣,但他似乎沒有很在意。
一月開始寫 LeetCode,三月開始嘗試面試,六月密集面試,整個過程大概半年。LeetCode 最後大概寫了 240 題,使用語言是 C++。 有蠻多人建議分類刷題,我自己是不太喜歡,因為會有先入為主的想法,比如說當你在寫 stack 這個類別的題目時,還沒看題目你就知道這題跟 stack 有關,但當面試時其實你不知道會遇到哪種題目,如果練習時就保持這種未知感,我自己覺得比較有幫助。 我自己是從某位大大分享的 Blind Curated 75 下手,有點像是 75 個基本題型,其他的題目多半是從這些來衍伸,基本題型寫完以後開始寫 CSpiration250 (這網站常常掛掉,可以搜尋 cspiration 關鍵字)。用一個 spreadsheet 做紀錄,遇到不會的或寫太慢的就標個記號過幾天再寫一次。另外練習邊寫邊講是一個很好的方式,平常我們比較不會這樣寫Code,但面試時重視的是你跟面試官之間的溝通,讓人家理解你的邏輯。 Linux 我是拿 jserv 大神的 Linux 核心設計系列講座 當作複習講義,再惡補一些 embedded system 常考題來準備。 Behavior questions 建議直接準備一次 Amazon 面試,因為 A 社超級重視這個,準備過一次其他間的 behavior questions 相對都輕而易舉。 最後,務必至少找人 Mock Interview 一次,非常非常有用。
45 common Amazon coding interview questions
nVidia Interview Process
- submit resume
- on-line assessment
- first interview with team manager (VP)
- second interviews with sr. solution architects
- confirm result
Interview Process
- The Initial Recruiter Screen
Interview Questions
2 rounds are work related. other 3 rounds are coding and algorithm
- Questions about hashmaps and related data structures
- Form a function to find max/min of 2 integers without using comparison operator.
/* The obvious approach to find minimum (involves branching) */
int min(int x, int y)
{
return (x < y) ? x : y
}
If comparison is not used, there is a simple mathematical logic behind it.
/*
* (big + small) + (big - small) = 2 * (big)
* big = ( (big + small) + (big - small) ) / 2
* (big + small) - (big - small) = 2 * (small)
* small = ( (big + small) - (big - small) ) / 2
*/
int max(int x, int y)
{
return ((x + y) + abs(x - y)) / 2);
}
int min(int x, int y)
{
return ((x + y) - abs(x - y)) / 2);
}
Access to static functions is restricted to the source file where they are declared.
Therefore, a static function has a scope that is limited to its object file.
Therefore, when we want to restrict access to functions, we make them static.
Another reason for making functions static can be reuse of the same function name in other files.
To resolve problems:
- 記憶體碎片化(Memory Fragmentation)
- 記憶體虛擬化(Memory Virtualization) 給每個 process 一塊獨立的虛擬記憶體(Virtual Memory),然後把他對應到可用的 實體記憶體(Physical Memory)中.
- Memory Management The modern CPU uses the hardware MMU to translate the virtual address to the physical address.
- kernel space memory access 做一個簡單的偏移就可以在實體地址和虛擬地址之間進行轉換
- user space memory access 每一個 process 有一個 page table,page table 儲存在記憶體中,執行時用 page table 的資訊來把 logical address 轉成 physical address。 page table的地址,都會儲存在其task struct的mm或者active_mm的pgd中。可以根據這個地址,按照頁表的分配方式來算。
logical address mapped to physical address
Each BAR corresponds to an address range that serves as a separate communication channel to the PCI device.
- Pointer to an integer
- Array of pointers
- Pointer to an array
- Function pointers
void (*function_ptr)(int); /* function pointer Declaration */
int sum(int num1, int num2);
int sub(int num1, int num2);
int mult(int num1, int num2);
int div(int num1, int num2);
int (*ope[4])(int, int);
ope[0] = sum;
ope[1] = sub;
ope[2] = mult;
ope[3] = div;
If this data is read again later, it can be quickly read from this cache in memory. The kernel maintains the internal data structure to optimize which data to be removed from the cache when the cache demands any additional space.
When the cache fills up, the data that has been unused for the longest time is discarded and the memory thus freed is used for the new data.
- page cache(file cache) The goal of this cache is to minimize file I/O.
- buffer cache(disk cache) The goal of this cache is to minimize block device I/O.
Its size is always 4KB.
They are usually 1 KB), directories, super blocks, other filesystem bookkeeping data, and non-filesystem disks are cached.
The typical example is a low priority process acquiring a resource that a high priority process needs,
and then being preempted by a medium priority process,
so the high priority process is blocked on the resource while the medium priority one executes (effectively being executed with a lower priority).
Because priority inversion involves a low-priority task blocking a high-priority task, one way to avoid priority inversion is to avoid blocking
The only way a new process is created by the kernel is when an existing process calls the fork() function.
The new process created by fork is called the child process.
Both the child and parent continue executing with the instruction that follows the call to fork.
The child is a copy of its parent:
- data
- heap
- stack
A fork is often followed by an exec. The child process will have the same environment as its parent, but only the process ID number is different.
A process can have multiple threads, all threads of the same process will share same PID.
A thread is a flow of execution through the process code, with its own program counter that keeps track of which instruction to execute next, system registers which hold its current working variables, and a stack which contains the execution history.
Processes run in separate virtual memory spaces.
A thread is a path of execution within a process.
Threads share with other threads their code section, data section, and OS resources (like open files and signals).
But, like process, a thread has its own program counter (PC), register set, and stack space.
Each thread has an associated scheduling policy and a static scheduling priority, sched_priority.
The scheduler makes its decisions based on knowledge of the scheduling policy and static priority of all threads on the system.
Conceptually, the scheduler maintains a list of runnable threads for each possible sched_priority value.
In order to determine which thread runs next, the scheduler looks for the nonempty list with the highest static priority and selects the thread at the head of this list.
Process that is not running appears in one of the following state:
- Runnable state (R) The scheduler keeps that process in the run queue (the list of ready-to-run processes maintained by the kernel).
- Sleeping state A process enters a Sleeping state when it needs resources that are not currently available.
- Interruptable sleep state (S) An Interruptible sleep state means the process is waiting either for a particular time slot or for a particular event to occur.
- Un-interruptable sleep state(D) An Uninterruptible sleep state is one that won't handle a signal right away.
- Defunct or Zombie state(Z) Between the time when the process terminates and the parent releases the child process, the child enters into what is referred to as a Zombie state.
When the CPU is available, this process will enter into Running state.
When the resource the process is waiting on becomes available, a signal is sent to the CPU.
The next time the scheduler gets a chance to schedule this sleeping process, the scheduler will put the process either in Running or Runnable state.
There are two types of sleep states:
It will wake only as a result of a waited-upon resource becoming available or after a time-out occurs during that wait.
The Uninterruptible state is mostly used by device drivers waiting for disk or network I/O.
The reason you cannot kill a Zombie process is that you cannot send a signal to the process to kill it as the process no longer exists.
- big-endian Big endian is how we normally deal with numbers: the MSB are placed leftmost in the structure (the big end).
Known as the "network byte order," the TCP/IP Internet protocol also uses big endian regardless of the hardware at either end.
0x100: 01 23 45 67 0x104:
0x100: 67 45 23 01
0x104:
The #error directive is often used in the #else portion of a #if–#elif–#else construct, as a safety check during compilation.
For example, the directives
#define BUFFER_SIZE 255
#if BUFFER_SIZE < 256
#error "BUFFER_SIZE is too small."
#endif
generate the error message:
BUFFER_SIZE is too small."
- Typical function call Only one copy of the function's instructions exist in the compiled program and those instructions are executed each time the function is called.
- macros The preprocessor expands macros by replacing the macro with the statements in the macro body.
- inline functions The compiler expands inline functions.
The function arguments are evaluated before they are passed to the function parameters.
For every occurrence of the macro call in the source code, there is a copy of of the macro body statements .
There is one copy of the function body for every function call in the source code.
The arguments are evaluated and the resulting value is passed to the function parameters before the expansion takes place.
- An integer
- A pointer to an integer
- A pointer to a pointer to an integer
- An array of 10 integers
- An array of 10 pointers to integers
(int *) a[10]
int (*a)[10]
int (*a)(int)
int (*a[10])(int)
int a[] = {6, 7, 8, 9, 10};
int *p = a;
*(p++) += 123;
*(++p) += 123;
Result:
129, 7, 131, 9, 10
#define dPS struct s * typedef struct s * tPS; dPS p1, p2; tPS p3, p4;Results:
struct s *p1, p2; (struct s *) p3, p4;
-
A type cast is basically a conversion from one type to another.
- Implicit Type Conversion All the data types of the variables are upgraded to the data type of the variable with largest data type. Signs can be lost (when signed is implicitly converted to unsigned),
unsigned int a = 6;
int b = -20;
(a + b > 6) ? puts("> 6") : puts("<= 6"); // > 6
The signed int will be converted to a very large unsigned int.
(type) expression
void reverseStr(string& str) {
int n = str.length();
for (int i = 0; i < n / 2; i++)
swap(str[i], str[n - i - 1]);
}
int main () {
int n;
cin >> n;
while (n >= 3)
n-= 3;
if (!n) cout << n << " is multiple of 3" << endl;
else cout << n << " is not multiple of 3" << endl;
}
x = 127:
01111111 127
01111110 126
127 & 126 = 01111110
x = 88:
01011000 88
01010111 87
88 & 87 = 01010000
This can be used to calclate the the number of bit in a number:
int count = 0;
while (x) {
x &= (x-1);
count++;
}
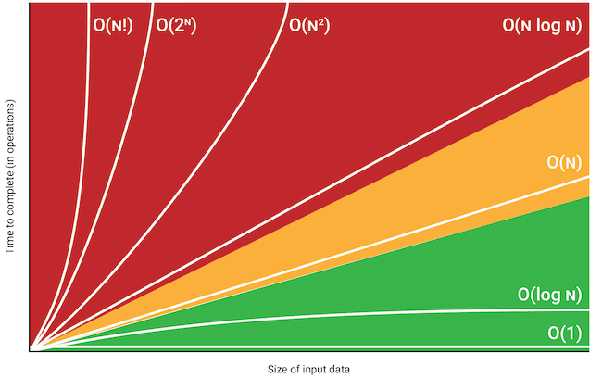






















留言